Partly circles
What is the same and what is different about these circle questions? What connections can you make?
Problem
Partly Circles printable sheet
Here are three problems involving circles.
Can you solve them?
Can you find relationships between the three problems?
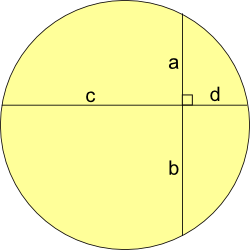
Firstly Show that ab = cd (where a, b, c, d are lengths)
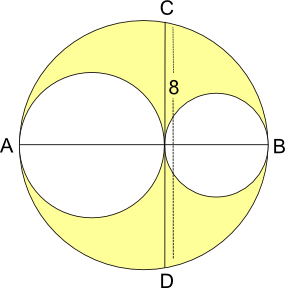
These three circles are drawn so that they touch each other, and their centres are all on the line AB.
If CD is $8$ units in length, what is the area of the region shaded yellow?
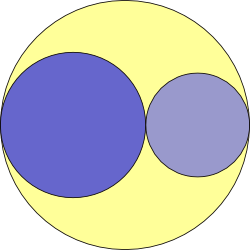
Lastly: If the area shaded yellow is equal to the area of the larger of the two blue circles, what is the relationship between the radii of the three circles?
Getting Started
Firstly:

Secondly:
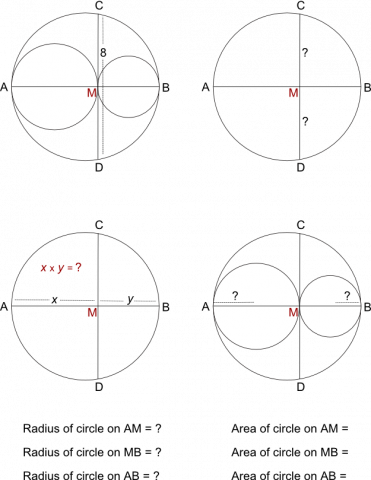
Thirdly:

Student Solutions
Well done to all those who sent in solutions to parts of this problem. We received a very clear and full explanation to all three parts of the problem from Daniel at Savile Park School, which you can see below:
Firstly:
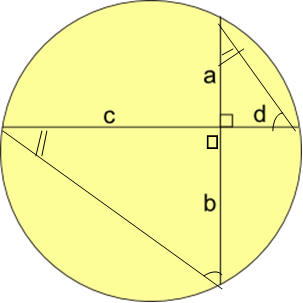
Join a to d, and b to c, to make two triangles. These triangles are similar because they have identical angles (angles in the same segment are equal).
So $ {a}\over{c}$ $=$ ${d}\over{b}$, which rearranges to give
$ab = cd$.
Daniel spotted that we do not need any numerical information to find a connection between the lengths, all we need to notice is that the triangles are similar!
Secondly:

Yellow Area $=$ Area of big circle $-$ Area of two smaller circles
Let the radius of the smaller circle be $r$, and the next circle be $R$. Then the radius of the big circle is $r+R$.
Yellow Area $=\pi (r+R)^2 - \pi r^2 - \pi R^2$
$=\pi ((r^2+2rR+R^2)-r^2-R^2)$
$=2\pi rR$
Using the result from the first part, if CD is halved, the product of the two halves is equal to the product of the diameters of the two smaller circles, so
$2r \times 2R = 4 \times 4$
$4rR = 16$
$rR = 4$.
But we know the yellow area is $2\pi rR$, so the yellow area must be $8\pi$.
Thirdly:

If the yellow area is equal to the larger of the two blue circles, we have
$\pi R^2 = 2\pi rR$
$R = 2r$
so the radius of the yellow circle is $r+2r=3r$
so the radii are in the ratio $1:2:3$.
To solve the second part of the problem, Daniel needed to take the step of working with algebra to find relationships. He then spotted that he could use the first part of the question to help him to an answer. The third part involved equating the area of the larger blue circle to the formula he had just found for the yellow area. Well done Daniel!
Teachers' Resources
Why do this problem?
This problem brings together some key ideas including the value of similar triangles, employing useful lines, some algebra and that problems can be solved even when information seems limited. The problem can also be used to make sense of other people's mathematical arguments. The aim of bringing the three problems together is to encourage discussion about their links and connectedness and therefore investigate relationships between problems and problem-solving experiences.
Possible approach
This printable worksheet may be useful: Partly Circles.
The first problem is designed to draw attention to similar triangles and to see that students may need to add lines to solve geometry problems.
Present the problem and give time for students to think about the problem and share ideas in a discussion. If ideas are not forthcoming suggest adding two lines (you might add them to the diagram without discussion) and then using angles in the same segment. If necessary spend some time adding and removing pairs of lines and talking about what is known about the triangles created:
- They are right-angled
- They have equal angles
- They are similar
Consider other ways of writing the result or substitute integers for three of the letters asking what the fourth must be (if a=$3$, b=$5$ and c=$6$ what must d be?)
The next two problems can be tackled in either order, and the images in Getting Started might help to stimulate discussion.
Once solutions for all three problems are available spend time discussing connections learners can make and those that are worth drawing particular attention to.
Key questions
What lines can you draw that highlight additional properties?
Can you identify similar triangles?
What do the first and second problems have in common?
How about the second and last problems?
Can you think of other problems where you have used similar ideas?
Possible support
Possible extension
Allow learners time to work on the problems with limited support and focus on what they see as "key moments" that helped them to solving the problems.
