Bend
What is the longest stick that can be carried horizontally along a
narrow corridor and around a right-angled bend?
Problem
Image
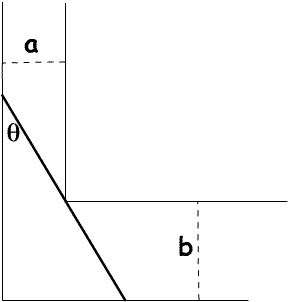
A long stick has to be carried horizontally along a narrow corridor and around a right-angled bend. The corridor is $a$ centimetres wide on one side of the bend and $b$ centimetres wide on the other side. Find, in terms of $a$ and $b$, the length of the longest stick that can be manoeuvered horizontally around the bend?
If the object is $2$ metres long and the two branches of the corridor are $65$ centimetres and $75$ centimetres respectively is it possible to manoeuvre the stick around the bend?
Getting Started
Work out the length of the straight line at an angle $\theta$ say
to one wall which just touches the inner corner in terms of $a,\ b$
and $\theta$. This length will change as $\theta$ changes and it
won't be possible to manoeuvre an object around the corner which is
longer then the minimum value of this length.
Student Solutions
Image

This solution comes from Andrei Lazanu ,Tudor Vianu National College, Bucharest, Romania.
I calculate the length of the stick in terms of $a$, $b$ and $\theta$. From the figure I observe that the length of the stick could be seen as the sum of two hypotenuses of two right-angled triangles. Its length is: $$l(\theta)= {a\over \sin \theta} + {b\over \cos \theta}.$$ Now, I have to calculate the minimum of this expression, in order to make the stick pass through the corner. For this, I calculate the derivative of $l(\theta)$ and equate it to $0$. I must say from the beginning that derivatives are not so familiar to me. For a minimum value of the length: $${\rm{d}l\over \rm{d}\theta} = {-a\cos \theta \over \sin^2 \theta} + {b\sin \theta \over \cos^2 \theta}=0.$$ So for a minimum value $a\cos^3 \theta = b\sin^3 \theta$ and $$\tan \theta = \left({a\over b}\right)^{1/3}.$$ Now, I have to calculate $\sin\theta$ and $\cos\theta$ as functions of $\tan\theta$. I know that: $$\cos x = {1\over \sqrt{1+\tan^2x}}$$ and$$\sin x = {\tan x \over \sqrt{1+\tan^2x}}$$ In the case of the problem, I have: $${1\over \cos \theta }= \sqrt{1+\left({a\over b}\right)^{2/3}}$$ and $${1\over \sin \theta } = \left({b\over a}\right)^{1/3}\sqrt{1+\left({a\over b}\right)^{2/3}}$$ So the minimum length is $$\eqalign{ {a\over \sin \theta} + {b\over \cos \theta} &=\left(a^{2/3}b^{1/3} + b\right)\sqrt{{a^{2/3}+b^{2/3}\over b^{2/3}}} \cr &= \left(a^{2/3} + b^{2/3}\right)^{3/2}}.$$ The result is symmetric in $a$ and $b$.
If $a=65 \text{ cm}$ and $b=75 \text{ cm}$ then $65^{2/3}+ 75^{2/3}=16.16623563 + 17.78446652=33.95070215$ and $33.951^{3/2}=197.8213407$ so an object of about $197 \text{ cm}$ could be manoeuvred around the bend but it is not possible to manoeuvre a $200 \text {cm}$ object around this bend.
Teachers' Resources
Some elementary calculus and trigonometry are required here and
some perseverance. You should expect the final answer to be an
expression symmetric in $a$ and $b$.
