Limiting probabilities
Given probabilities of taking paths in a graph from each node, use
matrix multiplication to find the probability of going from one
vertex to another in 2 stages, or 3, or 4 or even 100.
Problem
Image
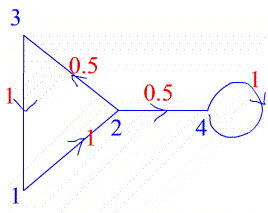
The numbers on the edges of this graph give the probabilities
of a particle travelling along those edges in the direction given
by the arrow. The same information is given by the entry $a_{ij}$
in the following matrix which gives the probability of travelling
from vertex $i$ to vertex $j$. $$A=\left( \begin{array}{cccc} 0
&1 &0 &0 \\ 0 &0 &0.5 &0.5 \\ 1 &0
&0 &0 \\ 0 &0 &0 &1 \end{array} \right)$$
For this question you can use a graphic calculator or computer
software to find powers of the matrices but you need to understand
the definition of matrix multiplication (see the Thesaurus) to be
able to do the question.
Can you see why the square of the matrix gives the
probabilities of travelling from one vertex to another in two
stages and the $n$th power of the matrix gives the probability of
traveling from one vertex to another in $n$ stages? For example $$
A^{20}=\left( \begin{array}{cccc} 0 &0 &0.008 &0.992 \\
0.008 &0 &0 &0.992 \\ 0 &0016 &0 &0.984 \\
0 &0 &0 &1 \end{array} \right) $$ This matrix shows
that there is zero probability of getting from vertex $1$ to vertex
$2$ in $20$ stages (that is along $20$ edges with the paths along
the edges being repeated), but there is a probability of $0.008$
(to 3 significant figures) of travelling from vertex $1$ to vertex
$3$ in $20$ stages.
Work out $A^{21}$ and $A^{22}$ and explain the occurrences of
zero and non zero entries in these matrices.
What would you expect to happen for higher powers, (e.g.
$A^{100}$), and why?
Getting Started
Think about the number of edges travelled when going around the triangle.
Student Solutions
Congratulations to Angus from Bexhill College; Richard from Bournemouth School and Andrei from Tudor Vianu National College, Bucharest, Romania for their clearly explained and excellent solutions to this problem.
Image

The numbers on the edges of this graph give the probabilities of a particle travelling along those edges in the direction given by the arrow. The same information is given by the entry $a_{ij}$ in the following matrix which gives the probability of travelling from vertex $i$ to vertex $j$. $$A=\left (\begin{array}{cccc} 0 &1 &0 &0\\ 0 &0 &0.5 &0.5\\ 1 &0 &0 &0\\ 0 &0 &0 &1 \end{array} \right)$$ This is Angus's solution. Firstly, we see that when we multiply matrices : $$ \left ( \begin{array}{ccc} A &B &C \\ D &E &F \\ G &H &I \end{array} \right) \left ( \begin{array}{ccc} a &b &c \\ d &e &f \\ g &h &i \end{array} \right) = \left ( \begin{array}{ccc} Aa+Bd+Cg & Ab+Be+Ch &Ac+Bf+Ci\\ Da+Ed+Fg &Db+Ee+Fh &Dc+Ef+Fi \\ Ga+Hd+Ig &Gb+He+Ih &Gc+Hf+Ii \end{array} \right) $$ and similarly for larger matrices. Hence when the matrix gives probabilities: $$A= \left( \begin{array}{cccc} P(1\to 1) &P(1\to 2) &P(1\to 3) &P(1\to 4)\\ P(2\to 1) &P(2\to 2) &P(2\to 3) &P(2\to 4)\\ P(3\to 1) &P(3\to 2) &P(3\to 3) &P(3\to 4)\\ P(4\to 1) &P(4\to 2) &P(4\to 3) &P(4\to 4) \end{array} \right)$$ where $P(1\to 2)$ is the probability of travelling to $2$ when at $1$. Then the first column of $A^2$ is: $$\left ( \begin{array}{c} P(1\to 1)P (1\to 1) + P (1\to 2) P(2\to 1) + P(1\to 3)P(3\to 1) + P(1\to 4) P(4\to 1)\\ P(2\to 1)P (1\to 1) + P (2\to 2) P(2\to 1) + P(2\to 3)P(3\to 1) + P(2\to 4) P(4\to 1)\\ P(3\to 1)P (1\to 1) + P (3\to 2) P(2\to 1) + P(3\to 3)P(3\to 1) + P(3\to 4) P(4\to 1) \\ P(4\to 1)P (1\to 1) + P(4\to 2) P(2\to 1) + P(4\to 3)P(3\to 1) + P(4\to 4) P(4\to 1) \end{array} \right ) $$ and so on for the four columns.
Now, the probability of getting from $1$ to $2$ in $x$ steps equals the sum of the probabilities of all the ways of getting from 1 to 2 in x steps : $P(1\to 2 \text{ (2 steps)}) = P(1\to 1)P(1\to 2)+ P(1\to 2)P (2\to 2)+ P(1\to 3)P(3\to 2)+\ldots$. Thus we have in $A^2$ the probability of getting from one point to another in two steps, as each entry in the matrix is the sum of probabilities of getting between the two points in two steps. Similarly, we find that if we cube the matrix, we are adding the probabilities of three-stage routes between two points, and so on for higher powers.
Now, we look at what happens for higher powers of $A$. $$A^{20}= \left( \begin{array}{cccc} 0 &0 &0.008 &0.992 \\ 0.008 &0 &0 &0.992 \\ 0 &0016 &0 &0.984 \\ 0 &0 &0 &1 \end{array} \right) $$ $$A^{21}= \left( \begin{array}{cccc} 0.008 &0 &0 &0.992 \\ 0 &0.008 &0 &0.992 \\ 0 &0 &0.008 &0.992 \\ 0 &0 &0 &1 \end{array} \right) $$ $$A^{22}= \left( \begin{array}{cccc} 0 &0.008 &0 &0.992 \\ 0 &0 &0.004 &0.996 \\ 0.008 &0 &0 &0.992 \\ 0 &0 &0 &1 \end{array} \right) $$ First (and easiest) we explain the fourth row. In the network, an object at vertex (4) has a probability of 1 of returning to (4) at the next journey. It therefore always returns to (4) and never reaches any other vertex. The fourth row will remain at $0$ $0$ $0$ $1$ as an object at (4) will remain at (4).
Next we come to the cycling of the three values in the loop at the left. At vertices (3) and (1), an object may only travel to one other vertex ((1) and (2) respectively), and at vertex (2) it travels to (3) (with a probability of $0.5$ which we ignore to explain the cycling). Therefore, an object at vertex (1) can travel to (2), then (3) then (1) again and so on. However, it moves on one vertex at a time so, if it cycles through the vertices, after n journeys the object will be at vertex $n (\text{mod } 3)$. Similarly, if it starts at (2), it will be at vertex $(n + 1)(\text{mod } 3)$ and, from (3), at $(n + 2)(\text{mod } 3)$.
Lastly, we explain the numerical values of the probabilities. Every time an object is at vertex (2), it travels to (4) with a probability p where p = 0.5 . Therefore, it will only avoid going to (4) with a probability of $(1 - p)^m$ , where $m$ is the number of times the object is at vertex (2) and $m$ is roughly $n/3$. Therefore, the probability of an object starting at vertices (1), (2) or (3) arriving at (4) is $1 - (1 - p)^m$ . As once the object is at (4) it cannot travel to any other vertex, the probability of being at (4) after n journeys can only increase.
With this information, we can predict the behaviour of $A^n$ as we let $n$ increase. All values in the fourth column will tend to one as $n$ tends to infinity, as they are given (roughly) by $1 - 0.5^{n/3}$ and $0.5^{n/3}$ tends to 0. The other nine values will cycle as shown above, in the manner : $$ \left( \begin{array}{ccc} 0 &a &0 \\ 0 &0 &b \\ c &0 &0 \end{array} \right) \to \left( \begin{array}{ccc} 0 &0 &b \\ c/2 &0 &0 \\ 0 &a &0 \end{array} \right) \to \left( \begin{array}{ccc} c/2 &0 &0 \\ 0 &a/2 &0 \\ 0 &0 &b \end{array} \right) \to \left( \begin{array}{ccc} 0 &a/2 &0 \\ 0 &0 &b/2 \\ c/2 &0 &0 \end{array} \right) $$ and so on for $n=3x+1,\ 3x+2,\ 3x+3,\ 3(x+1)+1$ respectively where $x$ is an integer.
The values of $a,\ b$ and $c$ will tend to zero as they are given by $0.5^m$ for $n$ stages where $m$ is of the order of $n/3$. Hence $$A^{100}= \left ( \begin{array}{cccc} 1 &1\times 10^{-10} &0 &0.9999999999 \\ 0 &0 &5\times 10^{-11} &0.99999999995\\ 1\times 10^{-10} &0 &0 &0.9999999999 \\ 0 &0 &0 &1 \end{array} \right)$$
Teachers' Resources
The question requires an understanding of the definition of matrix multiplication and of the probability formulae $$p(u\ {\rm and}\ v) = p(u)\times p(v)$$ and $$p(u\ {\rm or}\ v) = p(u)+ p(v)$$
You will want to use a calculator (or software) that will work out matrix products for you.
