All tied up
Problem
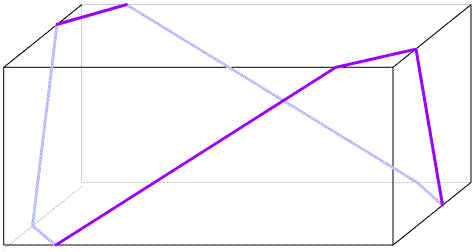
I like to run a ribbon around the box so that it makes a complete loop with two parallel pieces of ribbon on the top (and on the bottom) of the box.
The ribbon crosses every face once, except the top and bottom, which it crosses twice.
The ribbon rests tightly against the box all the way round because the angle at which it meets a corner is continued onto the next face.
I can cut the ribbon in advance of placing it around the box and I can slide the ribbon around a little to position it.
If the box is $20 \text{ cm}$ by $10 \text{ cm}$ by $5 \text{cm}$ - how long will the ribbon be?
Show why it is possible for me to "slide" the ribbon.
What will it be for any box with height $h$, width $w$ and length $l$? (n.b. the length and width are the longer distances and form the top of the box. Would the string be longer or shorter if this was not the case?)
Getting Started
Try looking at the net of the box.
Student Solutions
A solution based on the one from Richard is given below. I was not able to use Richard's original diagram but hope the one submitted is sufficient:
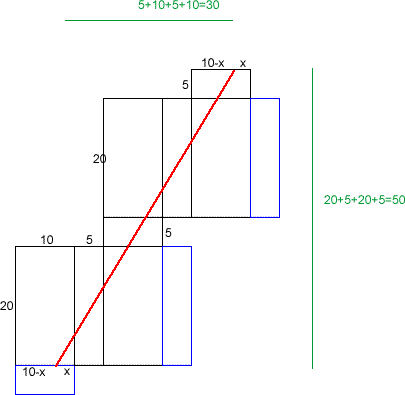
As the path of the ribbon around the box does not change direction when it reaches each edge, it can be drawn as a single straight line. As the ribbon crosses two faces of the box twice, a simple net of the box can show the path as a single straight line.
I therefore numbered the faces 1-6 and checked the order the ribbon went over them. This led to the diagram submitted, which I used to work out the length of the ribbon via Pythagoras' theorem.
The length of the ribbon is given by:
$$ \sqrt{(2 \times 5 + 2\times 10)^2 +(2 \times 5 + 2\times 20)^2}$$
By rearranging the above and substituting W, L and H for thelengths of the sides, the general expression for the length of the ribbon is therefore:
$$ 2\sqrt{(W+H)^2 + (L+H)^2}$$ or $$ 2\sqrt{W^2 + L^2 + 2H^2 + 2(WH + LH)} $$
where $H$ is the length of a shortest edge of a box, $W$ and $L$ the lengths of the longer sets of sides.
A little more from Andrei - many thanks:
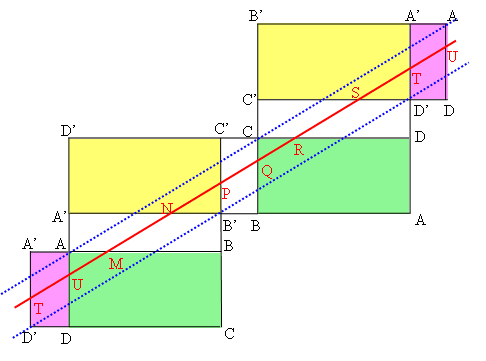
The condition of the problem is matched only when the red line passes through the same $U$, i.e. the dashed blue passes through the same $A$. So, the length of the ribbon is the distance $A$-$A$.
The blue dashed lines are the extreme positions of the ribbon, and between these positions the ribbon could glide. Each of these extreme positions has one of the two parallel lines reduced to a point.
Teachers' Resources
The problem "The Spider and the Fly" is worth trying first if you do not know where to start.
