Building BLOCKS
Here are some pictures of 3D shapes made from cubes. Can you make these shapes yourself?
Problem
Here are some pictures of 3D shapes made from cubes. Can you make these shapes yourself?
What do they look like from different positions? Please send us photographs or pictures of your models.

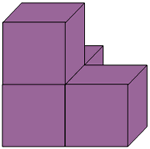
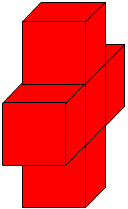

Getting Started
Try using multilink cubes.
Try starting at one end of the shape and adding a cube at a time.
You can look at each shape from above or from the sides.
Student Solutions
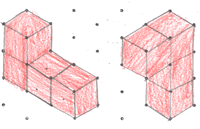
Thank you to Emma, Hannah, Shawnee and Sophie from Oakwood Junior School Maths Club for the drawings you did of the shapes. They explained that they made the shapes and put them at different angles, then copied them onto isometric paper. Here are some examples that Emma and Sophie drew for the first shape:
Image
| Image

|
Here is Sophie's drawing of the second shape:
Emma drew the third shape like this:
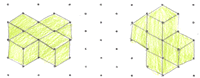
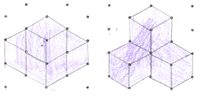
Finally, they both drew different versions of the fourth shape:
Image
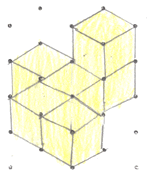
| Image
|
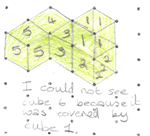
Ms Hope from Harrow School Beijing in China sent in these pictures of her pupils' models.




Thank you for those arrangements.
Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible extension
Possible support
