Inside Seven Squares
What is the total area of the four outside triangles which are outlined in red in this arrangement of squares inside each other?
Problem
Seven squares are set inside each other. The centre points of each side of the outer square are joined to make a smaller square inside it and so on.
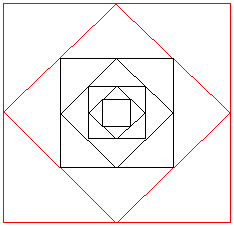
The centre square has the area of $1$ (one) square unit.
What is the total area of the four outside triangles which are outlined in red?
This problem is also available in French: Les 7 carrés
Click here for a poster of this problem.
Getting Started
You could draw it out on squared or dotty paper starting with the centre square.
Think about the scale - what size could you draw the centre square to make it easier to draw the others?
How does the second square compare in size to the centre square?
Student Solutions
You have found several different ways of answering this problem which is great. Many of you, including Fiona at Tattingstone School and Douglas at Burgoyne Middle School, decided to draw the squares. However, your approaches weren't necessarily the same.
This is what Fiona says:
The first thing I did was to get some squared paper to draw the figure on. I found out I couldn't start the middle square as one square because I couldn't draw the other squares accurately so I did the middle square as a four and that gave me points for the rest of the figure.
Image
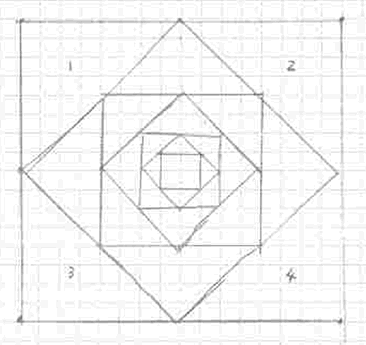
| To find the total area of the numbered triangles: I noticed that $1$ and $4$ were two halves of a square and also $2$ and $3$ are two halves of a square. |
Image
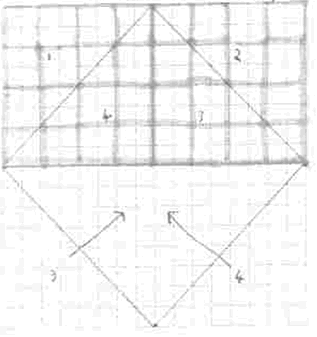
| Now I just have to count every square in this top rectangle as one unit: My answer is $32$ square units. |
Courtney, Charlotte and Tyler from Gateway Primary also used this approach.
Here is what Douglas did:
Gemma and Nathalie from City of London Freemen's School, Roger, Mark and Sam from Spalding Grammar School and George from Strand on the Green Juniors also noticed this pattern and so they didn't need to do any drawing to find the solution. Nathalie wrote:
Well done too to Callum from Arthur Mellows Village College and children from Truscott Street Public School.
Teachers' Resources
Why do this problem?
This problem provides a challenge when you are focusing on drawing lines and shapes accurately, or finding areas either by counting squares or calculation. The problem calls on learners' understanding of squares and right-angled triangles, and requires working systematically, as well as visualisation and reasonably accurate drawing.
Possible approach


Key questions
Possible extension
Learners who find this problem straightforward could find the area of each of the successive squares in the diagram and predict the size of the next squares, or try the problem Fitted, and/or Baravelle.
Possible support
Children could start with a $4 \times 4$ square and then draw a second square at $45^o$ to this with each side centred on a corner of the first square. Each side of this second square will be placed diagonally across two squares. A third and successive squares can be drawn in the same way.
