Fractional Triangles
Use the lines on this figure to show how the square can be divided into 2 halves, 3 thirds, 6 sixths and 9 ninths.
Problem
Use the lines on this figure to show how the pattern of triangles can be used to divide the square into two halves, three thirds, six sixths and nine ninths.
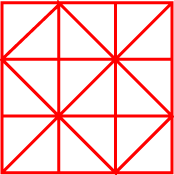
More lines are needed to divide it into four quarters.
What is the least amount of line needed to do this if the quarters are in one piece and all the same shape?
How many ways can you divide it into halves using just the lines given?
You might like to try out your ideas below.
Click on a dot to choose a colour, then click on a triangle.
Getting Started
What fraction of the design are the small squares?
How many sixths are there in a third?
You may like to print off this sheet for you to work on.
Student Solutions
Chris and Jenny sent us some colourful diagrams to show their answers:
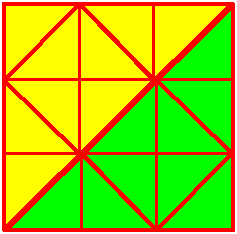
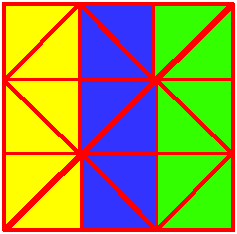
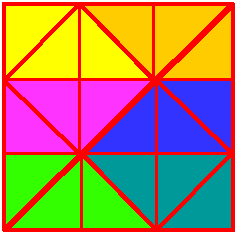
Julia drew on the line she'd draw to get quarters. Can you see that there are now four identical triangles? (Concentrate on the thickest lines.)
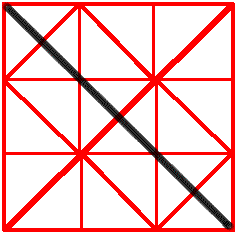
However, Anna wrote to say:
The least amount of line needed is one line dividing the central two triangles of the square in half.
I knew that the diagram had 18 triangles which is a number not divisible by 4. So I divided two triangles in half to have a total of 20 triangles which is a number divisible by 4. At first I drew the smaller triangles at the side of the square but this did not work. Then I divided all of the triangles in half using 9 lines giving me 36 triangles. I successfully divided the diagram into equally sized quarters of the same shape, but this did not give me the smallest amount of line. Once more I split two triangles in half but this time the halved triangle was in the middle.
There are lots of ways to divide the shape up into two halves. Sunita and Raj sent us two that they thought were nice:
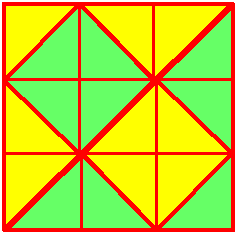
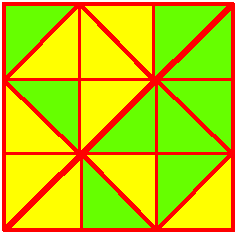
The Maths Challenge Group at St Aidan's VC School also sent us some different ways of dividing the shape into two halves. Here are the images they sent:
They told us:
We all compared our answers and came up with these as our final results. We looked very carefully at 5 and 7, 3 and 6 in order to be sure that they were different answers not merely a rotation. We are happy with our results after our discussion.
Thank you for sharing that with us and well done everyone.
Teachers' Resources
Fractional Triangles
Use the lines on this figure to show how the pattern of triangles can be used to divide the square into two halves, three thirds, six sixths and nine ninths.
More lines are needed to divide it into four quarters.
What is the least amount of line needed to do this if the quarters are in one piece and all the same shape?
How many ways can you divide it into halves using just the lines given?
Why do this problem?
This problem could be used as part of a lesson on finding fractions of various shapes. It should help develop an understanding of the relationship between the part and the whole. It allows children to explore fractions in a non-threatening, open-ended way and yet it does contain some real challenge.
Possible approach
This sheet (which contains six copies of the image) could be used both to work on and record answers to the problem. Coloured pencils would be useful to emphasise the different shapes within the design.
Key questions
Possible extension
Children could explore the design further and find the fraction of other shapes within the design such as the diagonally placed squares formed by four small triangles.
Possible support
Those experiencing difficulty with this problem may find it easier to start by looking at a $3 \times3$ grid. Even if the rest of the class are not using it, this sheet could be useful. Some learners may find it helpful to cut out the different fractions of the square to check that they are identical. (If this is the case, several copies of the image will be needed!)