Marvellous matrix
Problem
This problem was written for new year $2002$.
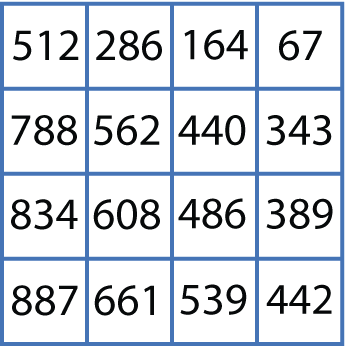
Circle any number in the matrix, for example, $608$ as below. Draw a line through all the squares that lie in the same row and column as your selected number.
Circle another number which has not got a line through it, for example, $343$ and again rule out all squares in the same row and column.
Repeat for a third time, then circle the remaining number which has not got a line through it.
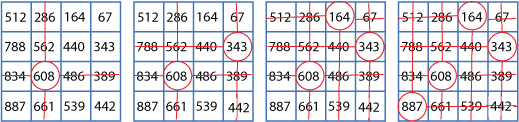
Add all the circled numbers together. Note your answer.
Try again with a different starting number. What do you notice?
See if you can work out how this matrix works.
Below is a simpler one which might be easier to investigate.
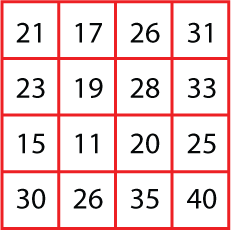
Can you make a similar matrix which generates a different total?
Getting Started
The matrix is generated from a matrix which looks like this:
Student Solutions
This proved quite hard to explain. Chris G and Chris B also from Moorfield Juniors had a good go:
In the end we worked out the diagonals=the target number (100) because each across does:
-4,+9,+5
and each down is:
+2,-8,+15
I noticed that selecting circled numbers in the way described gives one number in each row and one number in each column. Combining these pieces of information tells us that the total will always be the same.
It doesn't matter what order we do the addition in, we'll end up with 21 + 23 + 15 + 30 + 0 + -4 + 5 + 10 = 100. It's very easy to construct other matrices with this property now: just pick numbers for the row and column headings that add up to the required total.
Tom from Bristol Grammar School also thought about this problem, and made some interesting observations:
Let us label our matrix rows A,B,C,D and columns 1,2,3,4, and let (A1) denote the value of the top-left square.
In circling four numbers in different rows and different columns, we select four squares Aa, Bb, Cc, Dd where (a,b,c,d) is a permutation of (1,2,3,4).
In this solution I shall prove the necessary conditions for the sum (Aa)+(Bb)+(Cc)+(Dd) to be the same for all permutations (a,b,c,d). Let us say (A1)+(B2)+(C3)+(D4) = n (so the sum on a diagonal is n) Now, suppose we have a permutation where (a,b,c,d)=(2,1,3,4).
We can reduce this to the above case by swapping the values of A1 and A2 and of B1 and B2 in the matrix, so now all our values lie on the diagonal. Our condition states that the sum must be the same, so if we consider the 2x2 matrix (A1, A2)(B1, B2), we can see that our condition holds only if the sums of the diagonals of this matrix are the same.
By repeated use of this swapping system we can transform our matrix into one where the circled values lie on our diagonal. Suppose a is not 1, then we can swap Aa with A1 and X1 with Xa (where X is the row with the circle in column 1). If b is not 2 we can swap Bb with B2 and Y2 with Yb (where Y is the row with the circle in column 2). Note that Y cannot be row A because we know its circle is now in column 1. We apply this once more to row C (if c is not 3) to complete the rearrangement. Note that, again, for this to actually work, it is necessary that (A1)+(Xa)=(Ax)+(X1) (and similarly for rows B and C), because we know that ultimately after the swapping is complete X1-> Xa-> Xx is going to end up on the diagonal, since it is circled.
Analysing this method of transformation onto the diagonal, it is clear that our condition will hold for all permutations if and only if for every rectangle in our matrix (of size greater than or equal to 2 x 2), the sum of the values in one pair of opposite corner squares is equal to the sum of the values in the other pair of opposite corner squares.
This is a property possessed by the two matrices given as examples, and any other matrix with this property will also obey the condition. It is also not necessary to restrict oneself to 4 x 4 matrices. Any square matrix can exhibit the same behaviour (the proof is merely induction on the aforementioned method).
Can you explain it more clearly or add anything to this? If you think you can then email us.
