Always Perfect
Show that if you add 1 to the product of four consecutive numbers the answer is ALWAYS a perfect square.
Problem
Always Perfect printable sheet - part 1
Always Perfect printable sheet - part 2
In this problem you will get the chance to discover some surprising results. Can you prove that they are always true?
Part 1(a)
Take two numbers that differ by 2, multiply them together and add 1 (so for example $5 \times 7 + 1 = 36$).
Try this for some more pairs of numbers which differ by 2.
What do you notice? Is this always true? Can you prove your conjecture?
After you've had a go at this problem you might like to take a look at what Claire and Charlie did:
Show Charlie's Method
Charlie drew an n by n+2 rectangle, then split it up and rearranged it to almost make a square...

Show Claire's Method
Claire expressed what she discovered algebraically: $$n(n+2) + 1 = n^2 + 2n + 1\\ \hspace{20mm} = (n + 1)^2$$
Part 1(b)
Now take two numbers that differ by 4, multiply them together and add 4
(so for example $5 \times 9 + 4 = 49$).
Try this for some more pairs of numbers which differ by 4.
What do you notice? Is this always true? Can you prove your conjecture?
Part 1(c)
Now take two numbers that differ by 6, multiply them together and add 9.
Try this for some more pairs of numbers which differ by 6.
What do you notice? Is this always true? Can you prove your conjecture?
Part 1(d)
Looking at your results for parts (a), (b) and (c) can you predict what you will have to add to the product of two numbers that differ by $8, 10, 12, ..., 2k$ in order to get a square number?
Can you write down a general statement? Can you prove this statement?
---------------
Part 2(a)
Now consider what happens when $1$ is added to the product of four consecutive numbers, for example $2\times 3 \times 4 \times 5 + 1 = 121$.
Try this for some other sets of four consecutive numbers.
What do you notice? Is this always true? Can you prove your conjecture?
After you've had a go at this problem you might like to take a look at what Claire and Charlie did:
Show Charlie's Method
Charlie noticed a relationship between the product of the first and last of the four consecutive numbers, and the solution:
$$2\times 3 \times 4 \times 5 + 1 = 121 = (10 + 1)^2$$ $$3\times 4 \times 5 \times 6+ 1 = 361 = (18 + 1)^2$$ He then used this to help him write the general rule algebraically and check that it worked
Show Claire's Method
Claire expressed what she was doing algebraically: $$n(n+1)(n+2)(n+3) + 1 = n^4+ 6n^3 + 11n^2 + 6n + 1$$ and then she tried to factorise this to find a squared expression
Part 2(b)
Now take four consecutive even numbers (or four consecutive odd numbers), multiply them together and add 16 (so for example $2\times 4 \times 6 \times 8 + 16 = 400$).
Try this for some more sets of four consecutive even (or odd) numbers.
What do you notice? Is this always true? Can you prove your conjecture?
Part 2(c)
Now take four numbers which differ by 3, multiply them together and add 81
(so for example $2\times 5 \times 8 \times 11 + 81 = 961$).
Try this for some more sets of four numbers which differ by 3.
What do you notice? Is this always true? Can you prove your conjecture?
Part 2(d)
Looking at your results for parts (a), (b) and (c) can you predict what you will have to add to the product of four numbers that differ by $4, 5, 6, ..., k$ in order to get a square number?
Can you write down a general statement? Can you prove this statement?
Did you know ... ?
Although number theory - the study of the natural numbers - does not typically feature in school curricula it plays a leading role in university at first year and beyond. Having a good grasp of the fundamentals of number theory is useful across all disciplines of mathematics. Moreover, problems in number theory are a great leisure pastime as many require only minimal knowledge of mathematical 'content'.
We are very grateful to the Heilbronn Institute for Mathematical Research for their generous support for the development of this resource.
Getting Started
Part 1
Have you tried some simple cases to see if there is a pattern?
Can you adapt Charlie's and Claire's methods to prove your conjectures for parts (b), (c) and (d)?
Part 2
How could you write four consecutive numbers?
Can you use a table/grid to help you factorise your expression?
In the video below, Claire shows how you could factorise a quartic expression.
Student Solutions
Part 1(a): Take two numbers that differ by 2, multiply them together and add 1 (so for example $5 \times 7 + 1 = 36$).
Nikita from Jersey College for Girls noticed a pattern:

Charles from Rugby School in the UK, Rin from Wren Academy in England, Mahdi from Mahatma Gandhi International School in India, Airi from Japan, Isabel from England, Nikita and David all proved Nikita's rule using algebra (Claire's method). This is Airi's work:
Let the two numbers be $x$ and $x + 2.$
Multiplying them and then adding $1$ results in $x(x + 2) + 1 = x^2 + 2x + 1.$ This is equal to $(x+1)^2.$
So the result is always equal to the square of the arithmetic mean of the two numbers. (The mean of the two numbers is $\frac {x+(x+2)}2=x+1$).
Mahdi's algebra was different:
Interestingly, if we let the average (or middle number) be $n$, then the two numbers which differ by $2$ will be $n-1,n+1.$
Multiplying the two and adding $1$ gives this:
$(n-1)(n+1) + 1 = n^2 - 1 + 1 = n^2$
A nice application of difference of two squares.
Part 1(b): Take two numbers that differ by 4, multiply them together and add 4 (so for example $5 \times 9 + 4 = 49$).
Nikita used some examples to find a pattern:

Mahdi used a diagram like Charlie's diagram, where the two numbers were $n$ and $n+4$ so the "number in between" would be $n+2$:
Siddharth from Bishop Vesey's Grammar School, Sutton Coldfield in the UK, Charles, David, Nikita, Rin, Isabel, Airi and Mahdi also used algebra to prove the rule. This is Siddharth's work:
We can express the two numbers which have a difference of $4$ as $x$ and $x+4.$ We need to multiply the numbers and then add $4$ on. Using our definition of the two numbers, we can write this process algebraically as $x^2 + 4x + 4.$
What I notice is that this process gives the square of the mean of the two numbers, $\left( \frac {2x+4}2\right)^2.$ This can be simplified to $x^2 + 4x + 4.$ This proves that if you multiply any two numbers which have a difference of four and if you add $4$ on, the result is always the square of the mean of the two numbers.
Again, Mahdi used different algebra:
Armed with the difference of squares ovservation, I took the two numbers to be $n-2, n+2$
Multiplying the two and adding $4$ (because $2^2$) gives this:
$(n-2)(n+2) + 4 = n^2 - 4 + 4 = n^2$
Here $n$ is the average of the two numbers that I took. For example, if the numbers which differ by four are $5$ and $9,$ then the addition of their product and $4$ would be $7$ squared.
Part 1(c): Take two numbers that differ by 6, multiply them together and add 9
Hannah from Dulwich College Beijing in China made this observation:
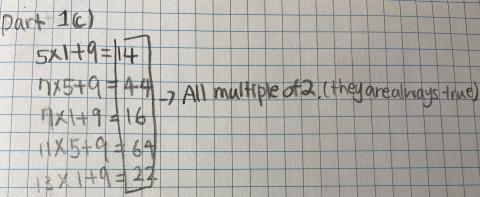
However, what if the two numbers are 2 and 8?
Nikita found a different pattern:
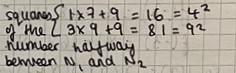
Charles, David, Nikita, Ria, Isabel and Airi proved the pattern continues. This is Charles's work:
Airi concluded:
So the result is always equal to the square of the arithmetic mean of the two numbers.
Part 1(d): Looking at your results for parts (a), (b) and (c) can you predict what you will have to add to the product of two numbers that differ by $8, 10, 12, ..., 2k$ in order to get a square number?
Rin and Nikita tried some examples and proved their results. This is Rin's work:
Difference of $8$:
$n(n+8)+a=(n+4)^2$
$a=4^2=16$
Difference of $10$:
$n(n+10)+b=(n+5)^2$
$b=5^2=25$
Difference of $12$:
$n(n+12)+c=(n+6)^2$
$c=6^2=36$
Difference of $2k$:
$n(n+2k)+m=(n+k)^2$
$m=k^2$
Multiplying two numbers with a difference of $2k$ and adding $k$ to the answer will give the square of these two numbers' mean.
$n(n+2k)+k^2$
$=n^2+2kn+k^2$
$=(n+k)^2$
Sanika from PSBMMS,OMR in India, David, Nikita, Isabel and Airi all wrote similar proofs.
Charles expressed the numbers in a slightly different way:
Once again, Mahdi used different algebra and a diagram:
(1) My method:
Since the two numbers differ by $2k$, the numbers can be $n-k, n+k$
Multiply the two numbers and add $k^2$ $$\begin{split}(n-k)(n+k) + k^2 &= n^2 - k^2 + k^2\\&=n^2\end{split}$$Note: the $n$ in my method is different to the $n$ in Claire's approach and Charlie's method
(2) by Charlie's method:
Part 2(a): Consider what happens when $1$ is added to the product of four consecutive numbers, for example $2\times 3 \times 4 \times 5 + 1 = 121$.
As Charlie suggested, Nikita used some examples to find a rule. Nikita then proved the rule:

Isabel noticed and proved a slightly different rule:
David proved the same rule in a different way:
Using Claire's approach, Mahdi, Rin and Airi started by using algebra. Rin wrote:
$n(n+1)(n+2)(n+3)+1\\= n(n+3)\times(n+1)(n+2)+1\\=(n^2+3n)(n^2+3n+2)+1\\=(n^2+3n)^2+2(n^2+2)+1\\=\left((n^2+3n)+1\right)^2\\ =(n^2+3n+1)^2$
Airi factoried the final term to get the same result as Nikita (using $x$ instead of $n$):
$=\left(x(x+3)+1\right)^2$
Part 2(b): Take four consecutive even numbers (or four consecutive odd numbers), multiply them together and add 16 (so for example $2\times 4 \times 6 \times 8 + 16 = 400$).
Nikita found and proved a rule:

Because Nikita's first number is $2n$, Nikita's proof only works when the numbers are even. Airi wrote a similar proof which works when the first number is odd or even:
$\begin{split}x(x+2)(x+4)(x+6) + 16 &= x^4 + 12x^3 + 44x^2 + 48x + 16 \\&= (x^2 + 6x + 4)^2 \\&= \left(x(x+6) + \sqrt{16}\right)^2\end{split}$
Isabel noticed and proved a different rule. Here is Isabel's work:
David and Sanika found and proved yet another rule. Sanika wrote:
The product of 4 consecutive even/odd numbers is equivalent to $$\begin{split}(x-3)(x-1)(x+1)(x+3)&=(x^2-9)(x^2-1)\\&= x^4-10x^2+9\end{split}$$Since $x^4-10x^2+9+16=x^4-10x^2+25=\left(x^2-5\right)^2$, the product of 4 consecutive odd/even numbers $+16$ will always be a perfect square.
David concluded:
The result will always be the mean of the four numbers, squared, minus 5, then squared again.
Part 2(c): Take four numbers which differ by 3, multiply them together and add 81 (so for example $2\times 5 \times 8 \times 11 + 81 = 961$).
Nikita found and proved a rule similar to her previous rules:

Isabel found and proved a rule similar to her previous rules:
David found the same rule as Isabel, but proved it using slightly different algebra:
We have
$(n-3)n(n+3)(n+6)+81\\=\left(n^2-9\right)\left(n^2+6n\right)+81\\=n^4+6n^3-9n^2-54n+81\\
=\left(n(n+3)-9\right)^2$
Sanika found a rule that was inspired by Sanika and David's rule in part (b). This is Sanika's work:
Product of four numbers with a consecutive difference of $3$ is
$(x-4.5)(x-1.5)(x+1.5)(x+4.5)$
[I chose this particular way so that I could get a complete the square sort of expression by simplifying this using the identity $a^2-b^2=(a+b)(a-b)$]
$=(x^2-20.25)(x^2-2.25)$
$=x^4-22.5x^2+45.5625$
Adding $81$ we get $x^4-22.5x^2+126.5625 =(x^2- 11.25)^2$
If the four numbers are whole numbers then $x$ will have a decimal of $0.5,$ in which case $x^2$ will have a decimal value of $0.25.$ Therefore the decimal value will cancel out with the $0.25$ in $11.25.$ Thus, $81$ plus the product of four numbers with a difference of three, will give us a perfect square (provided that the numbers are integers).
Part 2(d): Looking at your results for parts (a), (b) and (c) can you predict what you will have to add to the product of four numbers that differ by $4, 5, 6, ..., k$ in order to get a square number?
Nikita found a general version of the rules she'd proved above:

Isabel found a general version of the rules that she'd proved above:
David found the same rule as Isabel, but proved it slighty differently:
$(n-k)n(n+k)(n+2k)+k^4\\=\left(n^2-k^2\right)\left(n^2+2n\right)+k^4\\=n^4+2kn^3-k^2n^2-2k^3n+k^4\\=\left(n(n+k)-k^2\right)^2$
Sanika found a general version of the rules that she'd proved above:
If the difference between the numbers is $n$, then the number that must be added to the product of the four numbers is $n^4.$
Proof:
If you are working with a difference of $n$, then you name your sequence as follows:$$\begin{split}\left(x-\frac{3n}2\right)\left(x-\frac{n}2\right)\left(x+\frac{n}2\right)\left(x+\frac{3n}2\right) &= \left(x^2-\frac{9n^2}4\right)\left(x^2-\frac{n^2}4\right)\\&=x^4-\frac{10n^2}4x^2+\frac{9n^4}{16}\end{split}$$For the expression to be a perfect square it has to be in the form$$(a-b)^2 = a^2-2ab+b^2$$(Here $x^4 = a^2$, $2ab=\frac{10n^2}{4}x^2$ and so on)
So this can be expressed as $(x^2-b)^2$ where $b=\frac{-2ab}{-2a}$ which in this case is $\dfrac{\tfrac{-10n^2}{4}x^2}{-2x^2}=\frac{10n^2}8$
$\therefore b^2=\dfrac{100n^4}{64}$
$\Rightarrow$We will have to add $\left(\dfrac{100n^4}{64}-\dfrac{9n^4}{16}\right)=n^4$ to the expression to make it a perfect square.
Mahdi, Rin and Airi also found general expressions. This is Mahdi's work, which is very similar to Rin's work:
Airi factorised the final expression so that it looks like Nikita's rule:
$\left(x^2+3kx+k^2\right)^2 = \left(x\left(x+3k\right)+\sqrt{k^4}\right)^2$
How could you factorise the final expression so that it looks like Isabel's rule or Sanika's rule?
Teachers' Resources
Why do this problem?
This problem offers an excellent context for observing, conjecturing and thinking about proof. It also offers an opportunity to discuss the relationship between geometrical and algebraic methods for representing how numbers behave - an engaging introduction to number theory.
Along the way, students have the opportunity of practising routine algebraic procedures. The first problem involves factorising a quadratic expression to get a perfect square, and the second problem involves factorising a quartic expression.
Possible approach
"Take two numbers that differ by 2, multiply them together and add 1. What were your answers?"
Write a selection of students' responses on the board.
"What do you notice?" The answer is always a square number. The answer is always the square of the number between the two chosen ones.
"Will this always happen? Can you explain why?"
Give students some time to discuss with their partner why the answers are always square numbers. Circulate and listen out for interesting insights.
"We've worked out what happens when you find the product of two numbers that differ by 2, and then add 1.
I'd like you to explain what happens when you:
- find the product of two numbers that differ by 4, and then add 4
- find the product of two numbers that differ by 6, and then add 9
- find the product of two numbers that differ by ...
"Start by testing some numerical examples before trying to generalise using the representations we've looked at. Can you prove your results?"
Key question
Is there a way to represent the product of the two numbers that will explain the patterns you noticed?
Possible support
Possible extension
Part 2 of the problem could be used as an extension activity.
