Catrina's Cards
How would you find out how many football cards Catrina has collected?
Problem
Catrina wants to know how many football cards she has collected.
She has filled up five pages of her scrapbook and on each page there are four cards.
Can you show how you would find out? You might draw a picture or do some jottings or...
When you have had tried something yourself, click below to take a look at what some other children did:
Kerstin
I drew a number line to help:
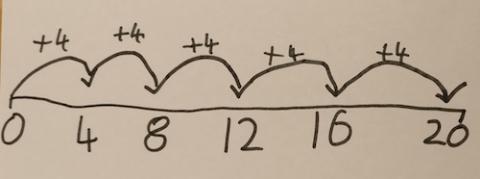
Isaac
I used counters to represent the football cards. I made an array:

Wai
I drew a picture:
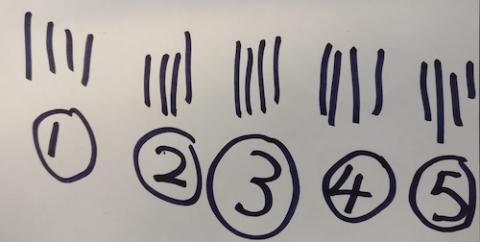
Danesh
I thought a double number line would help me work out the answer:
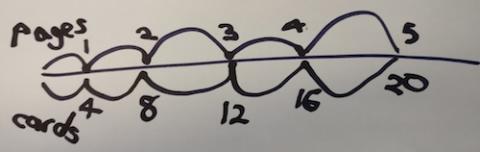
What is the same about the four ways? What is different?
How does each way compare with what you did?
Which one do you prefer and why?
Getting Started
You really can draw or write anything you like to help.
And/or how about using some equipment to help?
Student Solutions
We had a few solutions come in which showed how Catrina could work out how many football cards she has.
Joshua from Haslingfield Primary School wrote saying:
I used olive stones in five groups of four and counted them.
Georgia from Woodlea Junior School said:
I think the best idea of how to do this would be in your head because it's just 5 x 4.
Shree from The International School Frankfurt in Germany sent in this:-
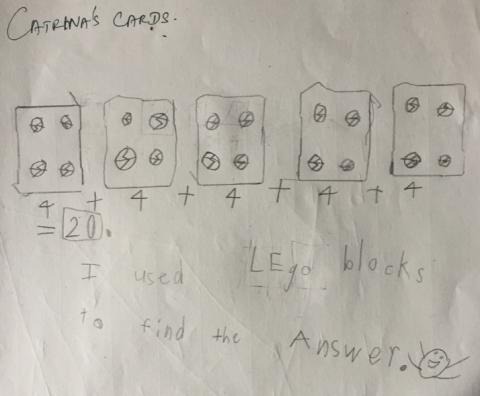
Thank you for these ways of calculating, maybe you can see other ways.
Teachers' Resources
Why do this problem?
Possible approach
You can then reveal the four different representations in turn. The order does not matter particularly, but you could choose one to start with that you have seen quite a few pairs adopting, if applicable. After showing each one, give pairs time to look at it carefully and compare it with their own representation. What is the same? What is different? You may want to invite a couple of pairs to share their thoughts with the whole group before moving on to the next representation.
Once the class has seen all four representations, invite them to compare all the different ways, including their own. You might find it useful to give out copies of this sheet, which has all four representations on it. In the plenary, draw out the similarities and differences (which may also involve sharing other representations that pairs have created themselves), and ask the children which they prefer and why. There is unlikely to be a consensus so it is important that individuals can explain what it is about that particular representation that they found useful.
Key questions
What is the same about these two representations? What is different?
What do they all have in common?
Possible extension
Possible support
Encourage children working in pairs to talk the problem aloud with each other.
