Six in a circle
Problem
A class of $30$ children were numbered from $1$ to $30$. Here are some of the class:

Their teacher set out a ring of $6$ chairs.
Child number $1$ sat on the first chair, child number $2$ on the second chair, child number $3$ on the third and so on going round the circle, up to child number $6$. The teacher then asked child number $7$ to stand behind child $1$, child $8$ to stand behind number $2$ etc. They continued this pattern until all the children were either sitting on a chair, or standing behind one.
How many people were standing behind each
chair?
Who was standing behind child number $3$?
What would happen if there were only $4$ chairs?
Getting Started
Perhaps finding a way to record this might be useful? How about using numbers $1$ to $30$ on bits of paper and arranging them?
Is there a link to factors and multiples which may help?
Student Solutions
We received two particularly good solutions to this problem. The first is from Helen and Daniela who go to Aldermaston C of E Primary School. They drew this table to help answer the questions:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 |
They therefore concluded that:
There are $4$ children behind each chair.
Children $9, 15, 21, 27$ were standing behind chair $3$.
Here's the table they drew for only four chairs:
| 1 | 2 | 3 | 4 |
| 5 | 6 |
7
|
8 |
| 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 |
| 29 | 30 |
They comment that:
Seven children are behind $1$ and $2$. Six children are behind $3$
and $4$.
There can't be the same number behind each chair because $30$
doesn't go into $4$ but $30$ goes into $6$. (I think perhaps you
mean that $4$ doesn't go into $30$, but $6$ does.)
The second was from Joe and Richard at St. Nicolas CE Junior School, Newbury who also drew a diagram to help them solve the problem:
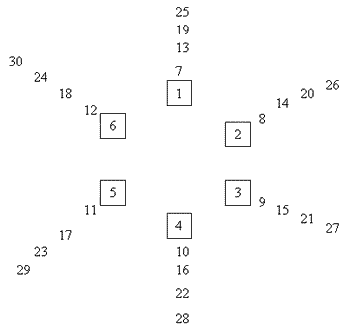
Joe and Richard say:
We started by drawing children round the circle like in our diagram
above. We answered the questions next.
1) Four people were standing behind each chair.
2) Behind number $3$, there were $9, 15, 21, 27$.
We made another drawing but with $4$ chairs and put the children round the circle. In the end, we counted the children up. $1$ and $2$ had $7$ children behind each and $3$ and $4$ had $6$ children. Then we noticed that however many chairs there were, the numbers went up by the highest numbered chair. We tested this solution by using $2$ to $6$ chairs and it worked.
We also noticed that on the last chair, the numbers go up in its table. We tested this on numbers of chairs from $2$ to $6$ and it worked with every single one.
We noticed that because $6$ is a factor of $30$ and $4$ isn't, $4$ didn't have the same number of children around each chair and $6$ did. Then we noticed the only numbers of chairs that would have an equal number of children behind each chair were factors of $30$, which are $1, 2, 3 ,5, 6, 10, 15$ and $30$.
Helen and Pauline from Moorfield Junior School also drew a chart. I think this was a useful strategy. Well done to everyone who answered this correctly and gave good explanations.
