A Square of Numbers
Can you put the numbers 1 to 8 into the circles so that the four calculations are correct?
Problem
Can you put the numbers $1$ to $8$ into the circles so that the four calculations are correct?
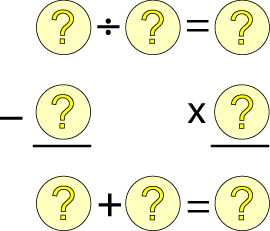
Getting Started
Which circles could contain the $1$?
What are the possibilities for the multiplication?
Student Solutions
We have been inundated with solutions for this problem - you obviously liked it! However, very few of you sent in a complete solution, but well done to Joshua, James, Arabella and Jessica from Aldermaston School who mentioned that:
The first thing was to figure that the one of the two biggest even numbers go in the bottom right corner and the other goes in the top sum with its half to make two so that the other numbers half is doubled to make it. One is important and always goes in the bottom left corner.
This is one good way to start and opens up the possibility of there being more than one solution. Alice from Tattingstone School also began in this way and explained that first she put 8 in the top left corner and worked through the other places from there. Clement from Sha Tin College sent a fantastic account of how he solved the problem:
Firstly, you have to find the top left number, only 4 numbers are divisible between 1-8: 2, 4, 6 and 8. Then go across the problem.
Among these, 2 is only divisible by 1 and itself, meaning that either the number 2 is divided by or the answer, will have to be 2 as well. So 2 is ruled out.
The next one, 4, is only divisible by 1, 2 and 4. Divided by 1 gives 4 again; divided by 2 gives 2 again; and divided by 4 would be a repeat. 4 is ruled out.6 can be divided by 2 and 3 (1 and 6 ruled out because they give repeats). If divided by 3, this gives the answer as 2, and now we look at the multiplication in the problem. Going down, 2 multiplied by 1 would be a repeat, 2 multiplied by 2 would be a repeat, multiplied by 3 would be a repeat, multiplied by 4 would give 8, which is OK. So 6 is possible at the top left corner.
Now we go back to 6, and do the subtraction going down. 6 can only be subtracted by the remaining numbers: 1, 5 and 7. 7 is bigger than 6 so that is ruled out. Subtracted by 1 would give 5, which when added to the last number remaining: 7, would give 12, not 8, as we have already worked out. So if it is 6-5, that would work since it gives 1, which when added to 7, gives 8. THIS IS THE FIRST SOLUTION.

We come to the second solution.
If we divide the 6 by 2, this gives 3. 3 (going down) multiplied by 1 would be a repeat, by 2 would give 6 again which has been used; by 3, that would be too big.So now we come to the last possible number that can be used at the top left corner: 8. 8 can be divided by 2 and 4.
If divided by 2, this would give 4, and 4 going down (multiplication) times 1 would give 4, a repeat; multiplied by 2 would give 8 which was used already; and multiplied by 3 would be too big.
So we move on to 8 divided by 4, which gives 2. 2 times 1 is a repeat; times 2 is a repeat; times 4 gives 8, which has been used. But 2 times 3 gives 6, which hasn't been used. So this is possible.Back to the other side, the subtraction of 8. 8 can be subtracted by 1, 5 or 7, the remaining numbers.
Subtracted by 1 would give 7 and 7 plus 5, the last number, would be too big.
Subtracted by 5 would give 3, which has been used.
Subtracted by 7 would give 1, which when added to the last number remaining, 5 gives 6. THIS IS THE SECOND SOLUTION.
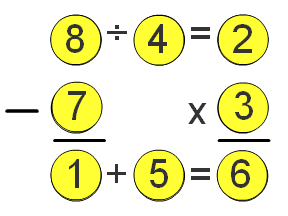
This is very clear, well done Clement. Another slightly different approach, but equally as good, was sent in by Alistair from Histon and Impington Junior School who wrote:
I gave each circle a letter so that would be easier to refer to them:
I found that B is not 1 because if it was, A would be the same as C. D and C cannot be 1 because the other one and E would be the same.
B can be 4, 3, or 2.
If B is 4, A = 8 and C = 2
If B is 3, A = 6 and C = 2
If B is 2, A = 6 or 8 and C = 3 or 4If C is 3, A is 6, but E would also have to be 6
If C is 4, A is 8, but E would also have to be 8Therefore C = 2.
If A = 6, B = 3, then D = 4 and E = 8
If A = 8, B = 4, then D = 3 and E = 6Whichever one is right, the numbers 2,3,4,6 and 8 are used, leaving 1, 5 and 7 for the remaining circles.
If A = 6, B = 3, C = 2, D = 4, E = 8 then F = 7, G = 1 and H = 5 is the only possibility for this combination.
If A = 8, B = 4, C = 2, D = 3, E = 6 then F = 5, G = 1 and H = 7 is another possibility.
Thank you Alistair. Well done too to Mr. Bullen's Brainiacs (Mr. Bullen's maths group) of Castle Primary School and Class 3 of Selside Endowed C of E Primary who also found both solutions. Mr Bullen's Brainiacs say they are working on the problem using a different set of consecutive numbers. What a good idea ...
Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible extension
Possible support
Having a copy of the problem on this sheet will be helpful for many children and giving them numbered counters to move around makes it easy to correct mistakes.
