Tetra Perp
Show that the edges $AD$ and $BC$ of a tetrahedron $ABCD$ are mutually perpendicular if and only if $AB^2 +CD^2 = AC^2+BD^2$. This problem uses the scalar product of two vectors.
Problem
A tetrahedron $ABCD$ has vertices $A$, $B$, $C$ and $D$, as shown below:
Image
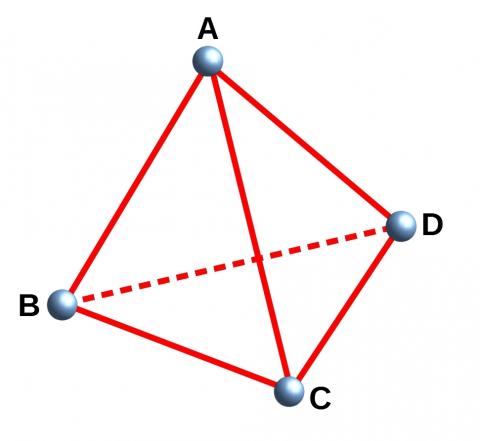
|
Show that the edges $AD$ and $BC$ of the tetrahedron are mutually perpendicular if and only if $AB^2+CD^2 = AC^2+BD^2$.
If the position vector of $A$ is ${\bf a}$ (and similar for the other vertices), can you use the scalar product to find an expression for $AB^2$?
It might be helpful to note that $AB^2=|\overrightarrow{AB}|^2$.
Sometimes it is easier to try and show $p-q=0$ rather than trying to show $p=q$.
Getting Started
If the length of vector ${\bf a}$ is $a=|{\bf a}|$, then we have $a^2={\bf a}\cdot {\bf a}$.
We have $\overrightarrow{AB}=\overrightarrow{AO}+\overrightarrow{OB}={\bf b} - {\bf a}$.
It might be easier to consider $(AB^2+CD^2) - (AC^2+BD^2)$ and show that this is equal to $0$ rather than trying to show that $AB^2+CD^2 = AC^2+BD^2$.
Student Solutions
Anya from Tanglin Trust School in Singapore sent in an elegant proof which didn't use vectors (click to enlarge):

Dylan from Brooke Weston and Joshua from Bohunt Sixth Form, both in the UK, used vectors. Joshua set out a good method for approaching the proof. However, Joshua made some assumptions about what the vectors a, b, c and d were, which means Joshua's proof is only valid for those cases. Click here to see Joshua's work.
Dylan proved the statement using vectors. Here is Dylan's work (click to enlarge):

Teachers' Resources
Why do this problem?
This is a surprising result, which on first glance looks like it might involve Pythagoras's theorem. In fact, Pythagoras' theorem can be used to prove that if the two edges $AD$ and $BC$ are perpendicular then we have $AB^2+CD^2 = AC^2+BD^2$, but using it to prove the opposite implication is trickier. This might provide a good opportunity to discuss the difference between "if" and "only if".
This is a good opportunity to show how vectors can be used to prove geometrical properties, and also to appreciate how the scalar product relates to the length of vectors. There are also opportunities to consider the distributive law over the scalar product.
Key questions
What is a position vector?
If the position vectors of $A$ is $\bf a$, and the position vectors of $B$ is $\bf b$ then how can we express the vector $\overrightarrow{AB}$?
If the length of vector ${\bf n}$ is $n=|{\bf n}|$, how can we express $n$ in terms of the scalar product?
How can we simplify $({\bf a} - {\bf b})\cdot({\bf a} - {\bf b})$?
