Roots and Coefficients

If xyz = 1 and x+y+z =1/x + 1/y + 1/z show that at least one of these numbers must be 1. Now for the complexity! When are the other numbers real and when are they complex?

Target Six

Show that x = 1 is a solution of the equation x^(3/2) - 8x^(-3/2) = 7 and find all other solutions.

This problem in geometry has been solved in no less than EIGHT ways by a pair of students. How would you solve it? How many of their solutions can you follow? How are they the same or different? Which do you like best?

Cube Roots

Stage: 5 Challenge Level:

We have to find values of c - d where:

$\begin{eqnarray} c & = &{(5\sqrt{2}+7)}^{\frac{1}{3}} \\ d & = &{(5\sqrt{2}-7)}^{\frac{1}{3}} \end{eqnarray}$

Looking first for real roots, note that

$ (5\sqrt{2}+7)(5\sqrt{2}-7) = 50-49 = 1 $ so $c^3d^3=1 $ and hence $cd=1$ .

Also

$c^3-d^3=14$ giving

$\begin{eqnarray} (c-d)^3 & = & c^3 - d^3 - 3cd(c-d) \\ & = & 14-3(c-3) \end{eqnarray}$

$c-d$ satisfies $x^3+3x-14=0,$ and this has only one real root $x=2$ . \[ x^3+3x-14 = (x-2)(x^2+2x+7) = 0 \] . $x^2+2x+7=0$ has complex roots $-1+i\sqrt{6}$ and $-1-i\sqrt{6}$ .

Hence

$x=c-d=2$ is the only real value of the given expression.

There will be altogether 9 complex values of

$c-d$ because c can take 3 values and d can take 3 values. Denoting the cube roots of unity by 1, $\omega$ and $\omega^2$ , where $\omega = \cos{2\pi/3} + i \sin{2\pi/3} $ , the nine required values are given by: $2, 2\omega, \omega^2, (-1+ i\sqrt{6}), (-1+i\sqrt{6})\omega, (-1+i\sqrt{6})\omega^2, (-1-i\sqrt{6}), (-1-i\sqrt{6})\omega, (-1-i\sqrt{6})\omega^2 $

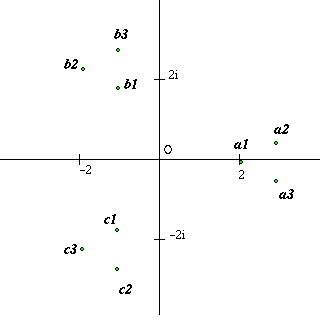
$(5\sqrt{2}+7)^\frac{1}{3} - (5\sqrt{2} - 7)^{\frac{1}{3}}$
$\begin{eqnarray} b_1& =& 2\omega \\ b_2& =& (-1-i\sqrt{6})\omega^2 \\ b_3 & = & (-1+i\sqrt{6}) \\ c_1& = & 2\omega^2 \\ c_2 & = & (-1-i\sqrt{6}) \\ c_3 & = & (-1+i\sqrt{6}) \end{eqnarray}$

Neil of Madras College found the complex values and dicovered some beautiful patterns when he plotted them in the complex plane. Neil's discoveries can be generalised to a ^1/3 - b ^1/3 for any real or complex numbers a and b, and from cube roots to n th . roots.

In order to find patterns similar to the ones discovered by Neil, but in a simpler situation, and to see how his ideas can be generalised, you may like to plot the twelve values of 8 ^1/3 + 81 ^1/4 in the complex plane.

Quadratic equations. Powers & roots. Interactivities. Complex numbers. Mathematical reasoning & proof. Complex roots of equations in conjugate pairs. Argand diagram. Modulus arithmetic. Surds. Index notation/Indices.

You may also like

Roots and Coefficients

Target Six

8 Methods for Three by One

Cube Roots

Stage: 5 Challenge Level: