Königsberg
Can you cross each of the seven bridges that join the north and south of the river to the two islands, once and once only, without retracing your steps?
Problem

Legend has it that the 'gentlefolk' of Königsberg would spend their Sunday afternoons walking around the town. It is believed they were attempting to cross each of the seven bridges, that join the north and south of the river to the two islands, once and once only without retracing their steps.
You might find it easier to study a more diagrammatic representation below (green dots represent the land to the north and south of the river and blue dots the two islands):
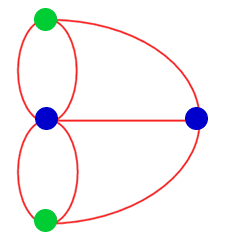
Can you succeed where the people of Königsberg failed, and solve the problem of the seven bridges? If not, can you explain why not? If you can, explain how you know that you have all the solutions?
Getting Started
Try drawing these maps without lifting your pencil
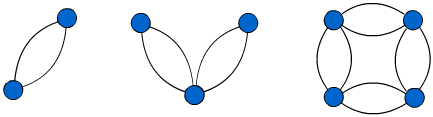
What do you notice about the start and end positions?
- Now consider these
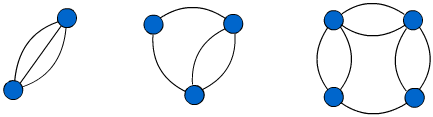
What do you notice about the start and end positions now?
Student Solutions
Thank you for all your solutions. I think it is quite difficult to explain the solution to this problem but many of you noticed the pattern of the nodes in the diagram and the importance of the fact that there are four nodes on the diagram, each of which has an odd number of routes from it.
The model of the town, where each island and each side of the river has an odd number of bridges leading to/from it, was included so that you could relate it to the diagrams in the hints. To be able to move from each of the four regions you must have two areas with an even number of bridges so that you can arrive and leave. Solutions received from Andrei of School 205 Bucharest, Alex and Joanna of Woodfall Junior School, Katherine, Phoebe and Katharine of The Mount School and Gowri, Hannah and Sophie of Caistor Grammar School used this idea.
The hints were there to help you to identify the importance of the number of odd nodes. It is worth going back to these and try to generalise your findings from this problem to other similar problems.
Andrei observed that the city is symmetrical in respect to a longitudinal line.
The journey is impossible.
Suppose the starting point of the walk is on a side of the river (it could be north or south, as specified the city is symmetrical); there are three bridges. The people must first go on the first bridge, return on the second, and then go away by the third, so they cannot come back! There must be an even number of bridges on each part so, that they can return home.
After solving the problem this way, I discovered that this is a famous problem of the history of mathematics, being at the basis of topology of networks, first developed by Euler in 1735. He constructed a diagram (essentially the same as yours), and associated the land with the vertices, and the bridges with the possible ways of connecting the vertices - arcs.
Using the reciprocal of Euler's theorem: "if a network has two or less odd vertices, it has at least an Euler path", that says "if a network has two or less odd vertices, it has at least an Euler path", it is easy to see that the proposed problem does not admit an Euler path (i.e. a continuous path that passes through every arc once and only once).
Teachers' Resources
You may like to download these notes which help to explain the diagrammatic representation and provides blank diagrams and maps with no bridges for further investigation.
This lesson plan suggests how you could introduce this problem in the classroom.
