You may also like
Summing Consecutive Numbers
15 = 7 + 8 and 10 = 1 + 2 + 3 + 4. Can you say which numbers can be expressed as the sum of two or more consecutive integers?
Always the Same
Arrange the numbers 1 to 16 into a 4 by 4 array. Choose a number. Cross out the numbers on the same row and column. Repeat this process. Add up you four numbers. Why do they always add up to 34?
Fibs
The well known Fibonacci sequence is 1 ,1, 2, 3, 5, 8, 13, 21.... How many Fibonacci sequences can you find containing the number 196 as one of the terms?
Age 11 to 14
Challenge Level
This problem follows on from More Number Pyramids.
These are top-heavy pyramids. The blue one has $21$ at the apex (top) and the red one has $31$.
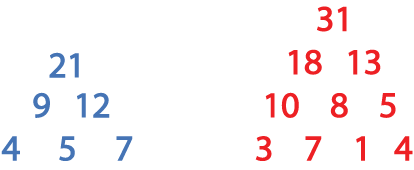
A pair of numbers are added to make the number above that pair.
In the blue top-heavy pyramid whose base is $4$, $5$ and $7$, $4 + 5 = 9$, so $9$ is placed between and above the $4$ and the $5$.
$5 + 7 = 12$ and $9 + 12 = 21$.
Use the numbers in the box below to make the base of a top-heavy pyramid whose top number is $200$.
NRICH is part of the family of activities in the Millennium Mathematics Project.