Semi-detached
A square of area 40 square cms is inscribed in a semicircle. Find the area of the square that could be inscribed in a circle of the same radius.
Problem
In the diagram below, the blue square is inscribed in the semicircle, and the yellow square is inscribed in the circle.
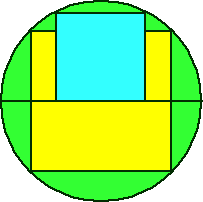
The blue square has an area of $40$cm$^2$.
Can you find the area of the yellow square?
Getting Started
Knowing the radius of the circle could be quite useful.
It might be helpful to draw the radius of the circle onto a diagram of the blue square.
Student Solutions
Correct solutions were received from Aashay of Farmington High, USA, Mary of Birchwood High School, Sana, Jenny, Chris and Rosion of Madras College, St. Andrews, Andrei of School 205 Bucharest and Chen of the Chinese High School, Singapore. Well done everyone!
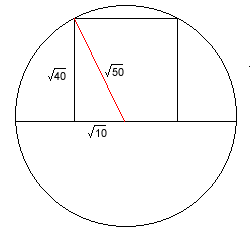
If a square has an area of $40$ sq units then its side is of length $ \sqrt{40} = 2 \times \sqrt{10}$.
Half the side is $ \sqrt{10}$.
So radius of the circle is $\sqrt{50} $.
Applying this to the square circumscribed by the whole circle (see below)
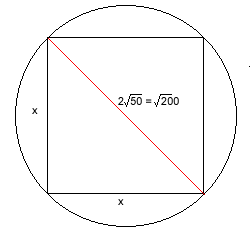
Diameter of the circle = diagonal of the square = $2 \times \sqrt 50 = \sqrt 200$
Let side of square $= x$ units. Area of the square = $ x^2$
Using Pythagoras' theorem:
$ x^2 + x^2 = 200 $
$ x^2 = 100 $
Therefore the area of the square is $100$ sq units.
Teachers' Resources
Why do this problem?
This problem could work well as a 'poster' - a visual challenge placed where students will see it. Or presented at the end of a lesson as something to try to solve.
Possible approach
This problem can worked well as something short and closed, but there is also an opportunity to invite questions which open up beyond the initial challenge. Finding the area of a square in a quadrant or squares fitted in the space between either of the two squares in the main problem and the circle.
Key questions
- What is the challenge and how might you start?
- How did you do it? Can you explain?
- How might you extend this problem?
- Can you calculate the area of squares fitted into other places within this diagram?
Possible support
Tilted Squares could be an excellent and accessible challenge for slightly less experienced students.
Possible extension
The approach suggested above indicates one route to extension within this context, or for another challenge fitting squares into shapes try Squirty. The problem Semi-square offers another opportunity to work out areas of squares inside circles.
