Dodecawhat
Follow instructions to fold sheets of A4 paper into pentagons and assemble them to form a dodecahedron. Calculate the error in the angle of the not perfectly regular pentagons you make.
Problem

We are going to make a pentagon. By making twelve such pentagons you can construct a dodecahedron like the one in the picture.
For each pentagon, you will need a piece of A4 paper and then follow the instructions below.
Image
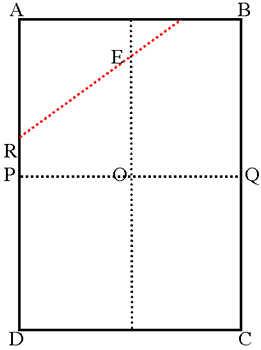
| Fold the paper in half both ways to find the centre O. Fold along the red line so A touches O. Fold C to O similarly. Fold B and D to O.
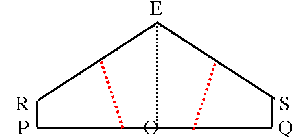
Next fold along PQ. As the two halves come together,tuck the flap from corner D behind the flap from corner B to make 'pockets' (see the diagrams below). Image
|
Fold R and S up to the centre line EO, so that they meet to form a straight line and make a pentagon.
If you make 12 pentagons in this way and assemble them, using your 'flaps' and 'pockets', you can make a dodecahedron.
Now for the problem:
A4 paper has sides in the ratio$\sqrt2$ to $1$.
If you use A4 paper for this construction and try to make regular pentagons there is a small error in the angle at E. Find this error and find the dimensions of the paper which you would need to use to get an accurate regular pentagon and hence an accurate regular dodecahedron.
Below is another series of instructions to fold a pentagon from a sheet of A4 paper:
Fold corner C up to corner A.
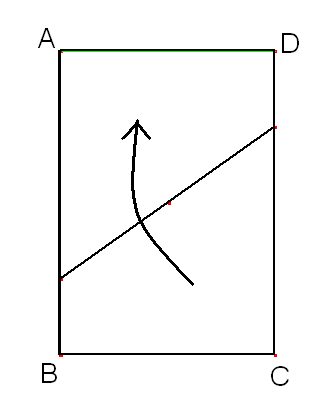
Your paper should now look like this:

Now lay edge BE along edge DF to create a mirror line. Mark the crease for the mirror but do not fold:
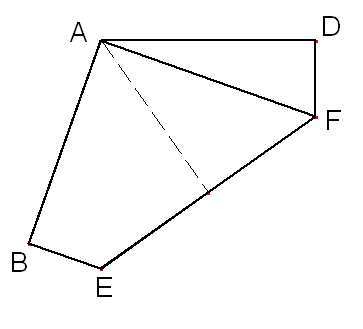
Lastly, fold edge BE to lie on the crease, then fold edge DF to lie on the crease.
If you do this you should get a pentagon like this:
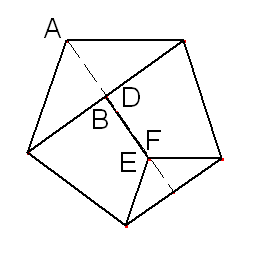
This pentagon might look quite different to the ones you made with the first series of folds, but the two shapes actually have the same angles!
Can you prove that the two different pentagons produced are similar?
How much smaller would my sheet of paper need to be to produce a pentagon the same size as my first ones?
Extra Resources:
1) You can construct other platonic solids using paper and this article explains how.
2) Have a look at the October 2000 Article titled Classifying Solids using Angle Deficiency
3) You can download a demo version of Stella , a computer program which lets you create and view polyhedra on the screen, then print out the nets required to build your own models out of paper. Small Stella and Great Stella are available from the Stella Website.
4) Alternatively, print out the models from this pdf available at the British Crystallographic Association's Website
Getting Started
Join AO in the first diagram. What is the angle between AO and the red fold line? Now find angle REO.
Student Solutions
Thank you Andrei from School No. 205, Bucharest, Romania for this solution.1
1. The angles of a regular pentagon must all be 108 °.
a) First I looked at the possibility of working with A4 paper.
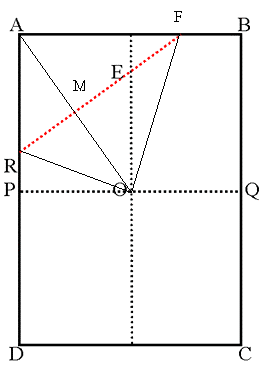
In the problem, I have to put A over O. So, triangles ARF and ORF are congruent, AM = MO and AO is perpendicular on FR.
As before, I note the smaller side of the paper (AB), with length x. Consequently, AD is $x\sqrt2$.
As P is on the middle of AD, AP = $x\sqrt2/2$. OP is x/2.
Triangle AOP is a right-angled triangle. As AP is parallel to EO, angles PAO and EOA are equal and, from the ratio of the side lengths of the paper, we get angle PAO = $tan^{-1}$ $(1\sqrt2)$ = 35.264 degrees.
As triangle MEO is also a right-angled triangle, angle EOM + angle MEO = $90^{\circ}$, so angle MEO is 54.736 degrees (to 3 decimal places).
But the figures (rectangle and then the pentagon) are symmetrical in respect to EO, so angle RES is two times angle MEO.
Angle RES = 2 $*$ MEO = $109.472^{\circ}$
The result is not $108^{\circ}$. The error is not so important, it is of the order of 1.4%
$${ {109.5^{\circ} - 108^{\circ}\over 108^{\circ}} = 1.4\%}$$
b) Now I have to calculate the new dimensions of the paper, so that I obtain a regular pentagon.
To make a regular pentagon in this way the ratio of the side lengths of the paper would have to be equal to tan 540 , that is in the ratio 1.376 to 1 (to 4 significant figures) rather than 1.414 to 1 as in A4 paper.
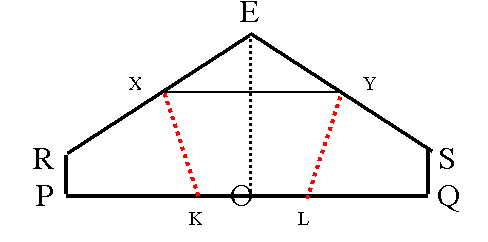
In the figure angle RES has a measure of 108 °, XY is parallel to PQ and XK and YL are angle bisectors of angles RXY and SYX respectively.
Angles EXY and EYX are both equal to 36 °. Consequently angles RXY and XYS both have a measure of 144 °. Now, I calculate angle KXY:
KXY = RXY/2 = 72 °
Now, I calculate angles EXK and EYL (the angles of the pentagon):
EXK = EYL = 72 ° + 36 ° = 108 °
I observe that the other two remaining angles are also congruent (by symmetry), both having a measure of 108 °.
So, I proved that in this case I obtain a regular pentagon.
Teachers' Resources
Why do this problem?
The stimulus for the problem is the engaging context of the construction of the solid. Is this really a regular dodecahedron and how can we be sure?
Possible approach
Key Questions
- How do you know this is a regular pentagon?
- What would have to be the case for the pentagon to be regular (all sides and all angles equal)?
- What do we know?
- What mathematics do you know that might be useful?
Support
Extension
