You may also like

problem icon

Writing Digits

Lee was writing all the counting numbers from 1 to 20. She stopped for a rest after writing seventeen digits. What was the last number she wrote?

problem icon

What Number

I am less than 25. My ones digit is twice my tens digit. My digits add up to an even number.

problem icon

One of Thirty-six

Can you find the chosen number from the grid using the clues?

6 Beads

Stage: 1 Challenge Level: Challenge Level:2 Challenge Level:2

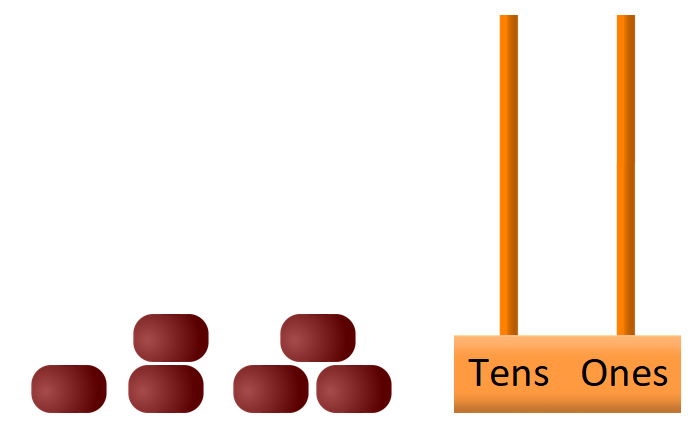
6 Beads


If you put three beads onto a tens/units abacus you could make the numbers $3$, $30$, $12$ or $21$.

abacus

 

Explore the numbers you can make using six beads.
pic4
 

 

Why do this problem?

This problem is a good, yet simple, activity that can get pupils thinking hard about numerals, numbers and place value.  It also provides a context in which to discuss different ways of recording.

Possible approach

You could start the children off by showing them one of the examples for three beads and then asking for other ways the beads could be arranged, reading the numbers together. You may want to use a basic drawing of the abacus on an interactive whiteboard and have 'beads' to drag into place. At this stage, you could encourage learners to try and explain how we know we have all the different ways.

After this the children could work in pairs on the six beads problem so that they are able to talk through their ideas with a partner. Have available a range of equipment which they could use, but allow them to make their own choice.  You may have, for example, a real abacus, counters, paper, beads, coloured pencils/pens etc. They could use digit cards to make the number which is represented on the abacus.

In the plenary, children could compare the ways in which they have recorded their findings and you could discuss the advantages of each. You could then talk about which recording methods would be best if we wanted to be sure that we had all the ways of using six beads. At this point, you could share any that have used such a system, or you could demonstrate your own way.


Key questions

What can you tell me about the numbers you've found?
Are there any other ways you can arrange those beads?
How can you tell if you have them all?

Possible extension

Learners could increase the number of beads or they could be asked to investigate what would happen if there were three columns: units, tens and hundreds.

Possible support

Some children may find it easier to use four beads, rather than going straight on to six. Using practical apparatus, such as counters, is essential for those having difficulties in understanding the problem.

The NRICH Project aims to enrich the mathematical experiences of all learners. To support this aim, members of the NRICH team work in a wide range of capacities, including providing professional development for teachers wishing to embed rich mathematical tasks into everyday classroom practice. More information on many of our other activities can be found here.
Copyright © 1997 - 2012. University of Cambridge. All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.