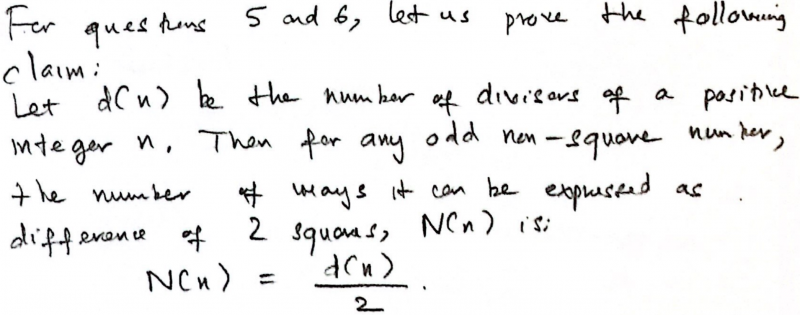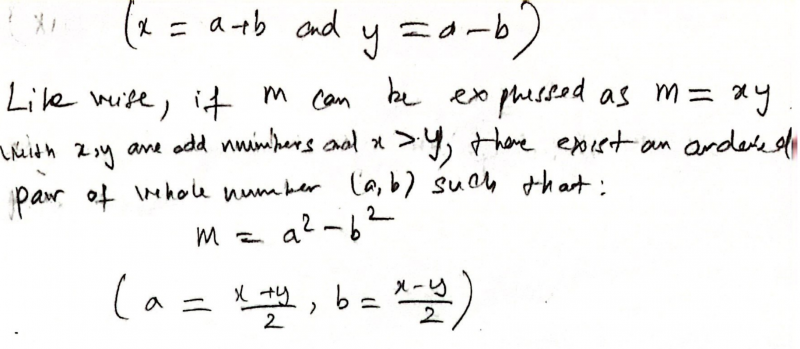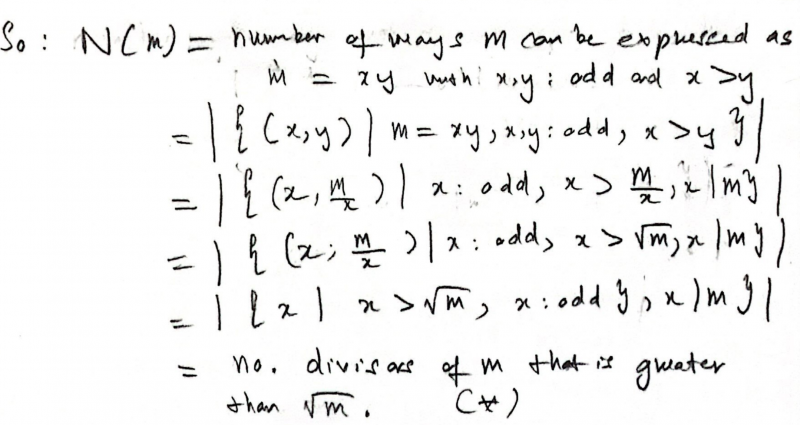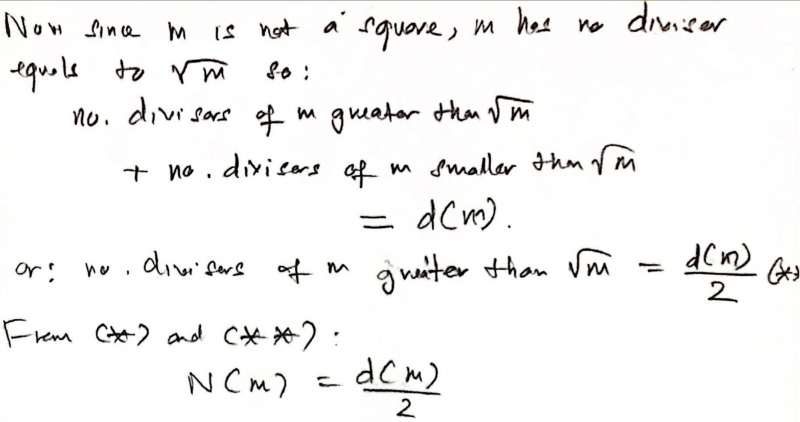Square Difference
Problem
All numbers referred to in this question are non-negative integers.
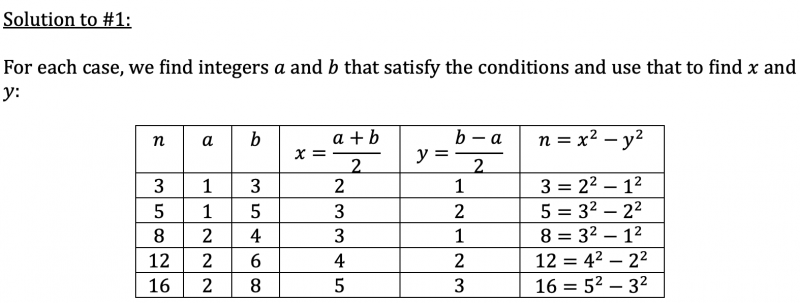
- Express each of the numbers $3, 5, 8, 12$ and $16$ as the difference of two non-zero squares.Can you notice any patterns in your answers? You could try a few more numbers as well. Are there any numbers that you cannot write as a difference of two squares?
- Prove that any odd number can be written as the difference of two squares.Have a look at your expressions for odd numbers in part (1), and try to express a few more odd numbers as a difference of two squares. Can you find a pattern that they all follow? Be careful - some numbers such as $21$ can be written as a difference of two squares in more than one way, and some ways won't fit the same pattern as the others.
Can you use algebra, or a diagram, to show that every odd number can be written as a difference of two squares (in at least one way!).
- Prove that all numbers of the form $4k$, where $k$ is a non-negative integer, can be written as the difference of two squares.If a number can be written in the form $4k$, then it is a multiple of $4$, i.e. $4, 8, 12, ...$
Again, look at patterns from your answers for $8, 12$ and $16$. Can you also express $20$ and $24$ as a difference of two squares? If we allow zero squares (which is ok in this part!) then we have $4=2^2-0^2$. Can you spot a pattern and use algebra or a diagram to prove that every number which is a multiple of $4$ can be written as difference of two squares?
- Prove that no number of the form $4k+2$, where $k$ is a non-negative integer, can be written as the difference of two squares.If a number has the form $4k+2$ then it is even, but it is not a multiple of $4$. For example we have $6=4\times 1 + 2$ and $34 = 4 \times 8 + 2$.
For this part you need to show that no matter what you do, you cannot make a number of the form $4k+2$ from a difference of two squares. You could start by considering the parity of a number of the form $A^2-B^2$, according to the different parities of $A$ and $B$.
*Considering the parity of a number means looking at whether it is odd or even.
- Prove that any number of the form $pq$, where $p$ and $q$ are prime numbers greater than $2$, can be written as the difference of two squares in exactly two distinct ways. Does this result hold if $p$ is a prime greater than $2$ and $q=2$?Examples might be helpful again. A good starting point is to consider $p=3$, $q=5$. Can you write $15$ as the difference of two squares in two different ways? It might be helpful to look back to your answer to part (1) for inspiration for one of the ways. You could also look at other examples.
Can you use your examples to make generalisations to prove that a number of the form $pq$, where $p$ and $q$ are primes greater than $2$, can be written as difference of two squares in two different ways.
The question asks you to show that it can be written as a difference of two squares in exactly two ways - can you show that there are no other ways of doing it?
If we have $pq=a^2-b^2$, can you use the difference of two squares formula to help you?
- Determine the number of distinct ways in which $675$ can be written as the difference of two squares.A good place to start is by writing $675$ as a product of prime factors. You might also want to include a factor of $1$.
STEP Mathematics I, 2014, Q1. Question reproduced by kind permission of Cambridge Assessment Group Archives. The question remains Copyright University of Cambridge Local Examinations Syndicate ("UCLES"), All rights reserved.
Student Solutions
Nishad from Thomas Estley Community College, Dylan from Brooke Weston, Steve from Dulwich College, Ziwei (Gilbert) from Stowe School and Joshua from Bohunt Sixth Form, all in the UK, Xuan Tung from HUS High School for Gifted Students in Vietnam, Dibyadeep from Greenhill School in the USA and Rishik K expressed each of the numbers $3, 5, 8, 12$ and $16$ as the difference of two non-zero squares. This is Rishik's work:
![]()
Nishad, Dylan, Joshua, Steve, Ziwei (Gilbert), Rishik, Dibyadeep and Xuan Tung proved that any odd number can be written as the difference of two squares. This is Dylan's work:
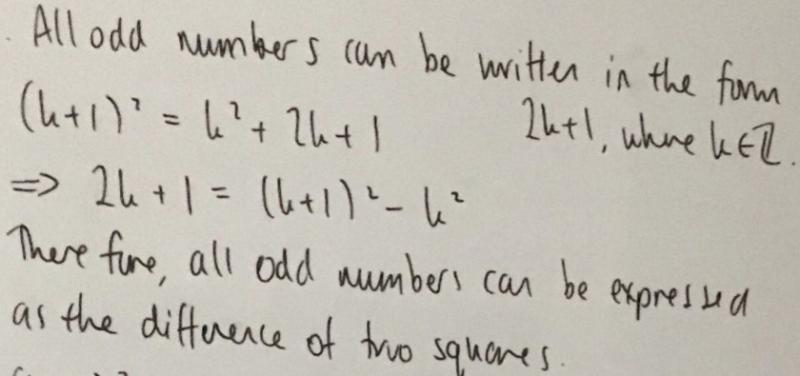
Dylan, Dibyadeep, Joshua, Steve, Ziwei (Gilbert), Xuan Tung and Nishad proved that all numbers of the form $4k$ can be written as the difference of two squares. This is Ziwei (Gilbert)'s work, which begins with an exploration (click on the image to open a larger version):
Nishad used a very neat factorisation of $4k$ to prove the statement:
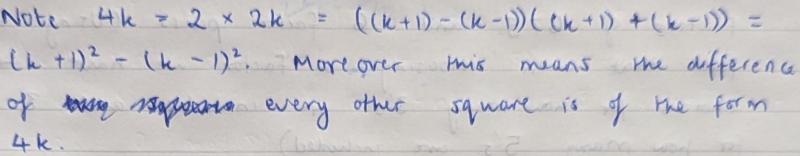
Nishad, Dylan, Joshua, Steve, Xuan Tung, Ziwei (Gilbert) and Dibyadeep all proved that no number of the form $4k+2$ can be written as the difference of two squares.
This is Dylan's proof:

Ziwei (Gilbert) and Dibyadeep thought instead about whether $a$ and $b$ (or "$x$" and "$y$") were odd or even. This is Ziwei (Gilbert)'s work (click on the images to open larger versions):
Dibyadeep went into even more possible cases:

To prove that numbers of the form $pq$ (where $p$ and $q$ are primes greater than $2$) can be written as the difference of two squares in exactly two ways, Ziwei (Gilbert) began with several investigations. This is some of Ziwei (Gilbert)'s work (click on the image to open a larger version):
Magnetoninja from the United States, Daniel from Dulwich College, Nishad, Dibyadeep, Dylan, Joshua, Steve and Ziwei (Gilbert) used this idea to prove the statement. This is Magnetoninja's work:
For integers $s$ and $t,$ WLOG (without loss of generality) let $s\gt t,$ the difference of the two squares $s^2-t^2=(s+t)(s-t).$
We claim that the two ways to write $pq$ such that it is the sum of two squares is to let $s-t=1$ and $s+t=pq,$ or to let $s-t=p$ and $s+t=q.$
Now we prove that this works for all primes $p$ and $q$ such that $p,q\gt2.$ We first consider letting $s-t=1$ and $s+t=pq.$ Substituting the first equation for $s$ in terms of $t$ into the second equation, we get $2t+1=pq.$ Note that $t$ can vary since we are only focusing on $p$ and $q,$ so it follows that $2t+1$ can be any odd number. Also, $p$ and $q$ must be odd since they are both primes greater than $2.$ This concludes the proof for our first case.
Next, we prove that $s-t=q$ and $s+t=p$ also works. Substituting the first equation for $s$ in terms of $t$ into the second equation, we obtain $q+2t=p.$ Once again, $t$ can vary so $2t$ can be any even number. Note that $p$ and $q$ are prime, therefore odd, so their difference will be an even number, proving our second case as well.
There are no more ways to write $pq$ as the difference of two squares since $p$ and $q$ are prime so $pq$ has only $4$ divisors and $2$ divisor pairs.
Can you see where Magnetoninja's cases would go wrong if $p=2$ or $q=2$?
Steve expressed $s$ and $t$ (or "$a$" and "$b$") in terms of $p$ and $q,$ and used this to write a clear explanation of why these results do not hold if $p$ is a prime greater than $2$ and $q=2:$
Natal from Canada started with this idea, and actually used this to answer the earlier questions. However, Natal does not find the second way to write $pq$ as the difference of two squares. Click to see Natal's work.
Xuan Tung extended the case of two primes $p$ and $q$ to any odd number that is not square. Click to see Xuan Tung's work.
Nishad, Dylan, Joshua, Daniel, Steve, Ziwei (Gilbert), Dibyadeep and Natal found the number of distinct ways in which $675$ can be written as the difference of two squares. This is Joshua's work:

Nishad, Dibyadeep, Ziwei (Gilbert), Natal and Xuan Tung showed that there are 6 ways without listing them all. This is Natal's work:


Teachers' Resources
This question asks students to investigate the different numbers they can make by considering the difference of two squares and to generalise their results. They will also need to prove that all numbers of a certain form can be made, and that it is impossible to make numbers of another form.
Students will probably need to use the following information
- Difference of two squares formula $a^2-b^2=(a+b)(a-b)$
- An even number can be written in the form $2k$, and an odd number in the form $2k+1$
- Facts about parity of numbers (for example an odd number multiplied by an odd number is odd)
- Uniqueness of prime factorisation
There are lots of suggestions for support for students in the What's Possible? Teacher notes.
Possible extension
Here is a list of number theory problems.
Students could also consider how they could write all numbers as a difference of two squares if they relax the "integer" condition.
How many ways are there to write any number as a difference of two squares?