Why dialogue matters in primary proof
Many young learners love exploring mathematical ideas and sharing their learning with others. Indeed, our Live Problems often attract a huge range of responses which draw on many different approaches. We're especially delighted when those solutions go beyond describing an approach, by explaining the thinking behind it. Sometimes these solutions might use words, or symbols, or both. These types of solutions are much more convincing for the reader and they are an essential step towards developing a watertight proof.
Many young learners seem to be natural conjecturers and convincers. We can encourage them to discover patterns and develop conjectures by asking questions such as 'What's the same, what's different?', and we can help them to use classroom manipulatives and their own drawings to explain their ideas to others. These key mathematical skills (identifying patterns, conjecturing, communicating...) are some of the essential building blocks of proof.
The Mathematics National Curriculum in England states that learners of all ages should:
"reason mathematically by following a line of enquiry, conjecturing relationships and generalisations, and developing an argument, justification or proof using mathematical language". (DfE, 2013)
Although experts differ in their definition of proof, the general consensus is that a proof needs to follow a logical argument to show that something is true or not true. This is something that even young learners can do really well using words. In this article, we will explore three essential features of proof, all of which can be developed in the context of primary mathematics. These features are based on the work of our colleague, Professor Andreas Stylianides, whose approach values the role of language in enabling young learners to make their own conjectures and convince others about their ideas.
1. Build your foundation
Mathematics has its own language and one of our roles is to support young learners to use it correctly, enabling our classes to avoid confusion and build strong arguments based on their understanding of key mathematical ideas. At primary level, this includes being clear about definitions, for example in the context of the 'special' numbers they come across in their lessons (odd, even, square numbers and so on), and common 2D and 3D shapes. This is not always as straightforward as it might seem. For example, how would you respond to the question "Is zero a prime number?". Have a think before clicking below to reveal our response.
How do you define a prime number?
A prime number is a whole number greater than 1, with exactly two factors - itself and 1. Therefore, zero is not prime.
Quite often when we discuss the properties of prime numbers in the classroom, we assume they must be greater than 1 without making that explicit.
Confusion can also reign because some mathematical words and phrases, including 'odd', 'take away' and 'mean' have different meanings in the real world. Encouraging our classes to agree the meaning of key terms and use them consistently is essential in preparation for creating a proof.
Hands-on experiences are essential - we need to allow learners sufficient time to explore, for example, sorting different shapes and playing with numbers. This practical exploration, coupled with a good grasp of mathematical language and exposure to robust definitions, enables them to progress towards making conjectures.
Having explored this activity, Matthew and Hannah from Stambridge shared their definitions of odd and even numbers:
Even numbers have two rows of the same number of blocks.
Odd numbers have one extra block in one of the rows.
Both of their definitions use only words, and they are very clear for the reader. This is a very good example of the sort of mathematical definition needed in readiness for the next step of a primary proof.
2. Formulate your argument
Having agreed the meaning of our key terms, we are now ready to use these foundations to form our argument to convince others about our answers. Again, these arguments can use words as a verbal representation rather than the letters associated with algebraic approaches.
Here is another solution we received for our Even and Odd activity, which came from Class 4SK from Devonshire Primary:
An odd number is a number with one left when we pair them up.
So if we add two odd numbers, the two left over can make a pair.
Can you see both the 'foundation' and 'formulation' in their argument? We suggest that the first line of their answer is clearly laying the foundations for their argument by defining an odd number. Their second line appears to offer a logical progession from their definitions. When they say, 'if we add two odd numbers, the two left over...' they have clearly generalised their ideas because they do not refer to any specific numbers. The class forms an argument about what they have observed using cubes to add any two odd numbers together. Their answer 'make a pair' also implies that they have formed similar definitions and understandings about even numbers.
3. Choose your representation
Looking at both solutions above, the learners have chosen to use verbal representations which have been transcribed. We suggest that verbal representations are very effective and age-appropriate for primary proof. They contain the key elements required for a proof - clear definitions, and logical arguments based on those definitions, which are presented in a convincing way for the reader.
Although verbal representations are ideal for younger ages, making excellent foundations for later algebraic approaches, comparing both approaches highlights their similarities and supports students' mathematical progression as they move through their schooling:
| Verbal Representation | Algebraic Representation | |
| Build your foundation | An odd number is a number with one left over when we pair them up | Odd numbers have the form 2n+1 where n is a whole number |
| Formulate your argument | So if we add two odd numbers, the two left over can make a pair |
Adding two odd numbers gives (2k+1) + (2m+1) = (2k+2m) + (1+1) = 2k +2m+1+1, which is even |
Looking at the two approaches, the verbal arguments might be age-appropriate, but they are also mathematically sound. They use the key features of a proof, namely clear definitions and a logical argument, building upon them to lead to a result.
This three-features approach can be used across a wide range of investigations, leading to proof. Another lovely example for younger learners is our School Fair Necklaces activity which also lends itself to a highly verbal approach (and there's an opportunity for more hands-on investigation too). Here is a reminder of the task:

They decided to make them very mathematical.
Each necklace was to have eight beads, four of one colour and four of another.
And each had to be symmetrical, like this.
One of the solutions we received was sent in by Lyneham Primary Junior Maths Challenge Group:
We used some different coloured counting blocks (unifix) to make symmetrical patterns of eight blocks with two colours.
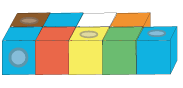
We figured out that with those blocks we could make six different combinations that were symmetrical (see picture). And then we figured out that it didn't matter if you cut half of it off because they are symmetrical, so the halves are exactly the same.
We found six different towers of four blocks, two of each colour (see at the bottom of the photo). So therefore there are six possible ways you can do it.
We suggest that their solution demonstrates some of the three key features of a proof using words (and, in this case, photos too!). Firstly, their solution has clear foundations because they clearly set out their approach exploring "symmetrical patterns of eight blocks with two colours" (see the black/white and orange/brown blocks in the picture above) and their definition of symmetry "it didn't matter if you cut half of it off because they are symmetrical, so the halves are exactly the same" (see the blue/green blocks at the bottom of the picture, each of which is half of a necklace). The children realised that they only needed to consider one half of the necklace, as long as they used two blocks of each colour in that half. Secondly, they begin to formulate their argument by stating that "We figured out that with those blocks we could make six different combinations that were symmetrical (see picture)."
The combination of words and cubes is at first very convincing: "We found six different towers of four blocks, two of each colour (see at the bottom of the photo). So therefore there are six possible ways you can do it." However, in order to constitute a proof they would need to go a little further. How do they know they have found all the possible ways? Are they certain that there are no more examples? It is interesting that, in the photo of the green and blue cubes, they appear to have placed the solutions in pairs - the first two examples on the left are 'opposites' of each other; so are the third and fourth; so are the fifth and sixth. Perhaps this hints at a system they have adopted to find all the possibilities, but they would need to explicitly mention their system in order for the reasoning to be completely watertight, and therefore constitute a proof.
In summary
As we have seen above using examples from number and geometry, young learners can be supported to create a convincing argument using words and pictures rather than symbols and equations. To help them to do so, we need to ensure that they use the relevant mathematical terminology correctly, and encourage them to present a logical argument for their audience. When they do so, their proofs with words can be just as convincing as the proofs with symbols developed by older learners.
Further reading
You may find these complementary NRICH resources useful:
Reasoning Feature, including an article Reasoning: The Journey from Novice to Expert, which outlines our five step progression in reasoning, culminating in proof
Mastering Mathematics: Developing Generalising and Proof Feature, including an article Mastering Mathematics: The Challenge of Generalising and Proof, which discusses different types of proof
References
DfE (2013) Mathematics programmes of study: Key stages 1 and 2 National Curriculum in England
Stylianides, A. J. (2007) "The Notion of Proof in the Context of Elementary School Mathematics." Educational Studies in Mathematics 65: 1-20
