Playing with Factors and Multiples
Why playing with factors and multiples matters
In 2009, a major supermarket chain found itself in court after disputing a payment totalling almost a million pounds for six mountain bikes. How did it find itself in such a position? The court case, which revealed that a simple mistake had resulted in the supermarket erroneously paying a retailer a thousand times more than usual for the bikes, highlighted the importance of nurturing and valuing number sense in both the classroom and our everyday lives.
Developing an intuitive 'feel' for numbers enables young learners to begin to make sensible estimates and identify obvious errors (such as an unexpectedly high payment for bicycles!), and flexibly apply their number skills in different situations. After all, 'without number sense, arithmetic is a bewildering territory in which any deviation from the known path may rapidly lead to being totally lost' (Dowker, 1992). At NRICH we believe that encouraging young learners to play with numbers throughout their primary schooling allows them to develop their number sense in a supportive, engaging environment.
It has been suggested that number sense 'develops continually as the range of known facts and the relationships among them are extended' (Anghileri, 2000). Hence supporting learners with their number sense goes far beyond enabling them to learn and apply their number bonds, it also requires them to understand the properties of numbers and the relationships between them, such as the relationship between factors and multiples.
Story telling and role play
Role play and story telling offer two playful approaches towards exploring number relationships with very young children. We have created a few Early Years activities that are based on books, each of which contains 'Using Books' in their title. Using Books: The Doorbell Rang features the well-loved tale by Pat Hutchins. At the start of this story a plate of freshly-baked cookies is given to two children, to be shared equally between them. As the story progresses, more and more children arrive to share the cookies. Can it be done? The activity offers a lovely context for very young learners to explore different ways to share a number of items. Their reasoning can be further explored through prompts such as 'What will happen if another person turns up now?', 'Can you explain why you think that? and 'Can you show me?'. There are more questions, additional teaching ideas, and links to further resources in the activity.
Once your class has enjoyed investigating ways to share cookies, another useful resource for exploring the concept of sharing equally is Maths Story Time which challenges young learners to help Pirate Panda share his 20 golden coins with his friends:
Pirate Panda has taken all the treasure, 20 golden coins.
Cat, Dog and Rabbit jump about excitedly, "Can we have some too?"
"No! No! No!" says Pirate Panda.
Can the children suggest what Panda ought to do?
Detailed notes are included in the activity suggesting ways to encourage very young learners to reason mathematically, and ways to further develop or vary the context to extend its potential in the classroom.
Making new discoveries

Purposeful play can lead to exciting new discoveries and help to address the seemingly insatiable curiosity of young learners. Moreover activities which have the potential to surprise young learners and make them curious about their world are ideal vehicles for developing their growing number sense. For example, Light the Lights offers a very motivating context for applying knowledge of number properties. The task features a machine with four coloured lights (pictured on the right), each light responding to a 'rule'. When learners type in a number, lights turn on if their rule is satisfied. Can learners work out the four rules? What is the smallest number that lights up all four lights?
This problem, which requires learners to make sense of information and work in a systematic way, has attracted the interest of both learners and their teachers. 'I love trying to get children engaged in tackling such problems' wrote one teacher. His class adopted a pattern-spotting approach towards solving the problem which you can explore in the Solutions tab of the task, alongside solutions submitted by other schools.
Exploring interactivities
A good knowledge of number properties can enable learners to work in different ways and check their answers, improving their accuracy and making connections in their learning. A very good example is using and applying divisibility tests. Dozens offers a twist on the usual way of assessing learners' knowledge of divisibility tests. Rather than asking learners to check whether a number is divisible by 2, 3, 4, 5... learners have to puzzle over the choices available as they are challenged to find the largest number that meets the necessary criteria.
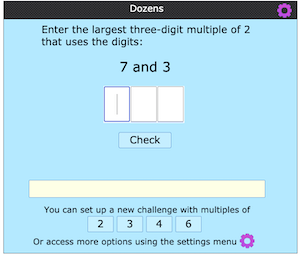
This low threshold high ceiling task has an accessible starting point, but then offers increasing levels of challenge as learners can opt to work with multiples of larger and larger numbers. Gabriel shared his strategies for identifying multiples of 3, 4 and 6:
"To find out if your number is a multiple of 3, all you need to do is add the digits. If the digits add up to a multiple of 3, the original number is also a multiple of 3.
For example: 351"
Taking things further, he reflected on the benefits of drawing on his growing number sense in the classroom:
"To find out if this is a multiple of 3 using normal division would be quite slow, but if you just add the digits it takes only a few seconds:
3 + 5 + 1 = 9
9 is a multiple of 3 so 351 is a multiple of 3."
Sometimes learners might find that it is impossible to meet the criteria. Reailsing that not every problem has a solution, and explaining why that might be the case, is another great opportunity for developing their number sense. Do look at the teachers' resources for this activity for ideas about how to introduce it in the classroom.
Being inventive
Developing a higher level of number sense enables learners to work flexibly, a skill which comes in very useful when exploring activities such as Dicey Array. This low threshold high ceiling game offers a meaningful and motivating context in which learners can deepen their understanding of factors and multiples, and develop their fluency with finding factor pairs. To get started, we suggest watching the video accompanying the activity which models how to play the game.

To play the game, players agree a target score to reach. Player 1 rolls the two dice and finds the total of the two numbers, they count out that number of counters and create as many rectangular arrays as they can using that total number of counters, scoring a point for each correct array. Then Player 2 takes their turn. Play continues like this with players taking it in turns to roll the two dice, and the winner is the player who reaches the target number of points first. This activity offers a playful, hands-on approach towards developing a much stronger number sense relating to factors and multiples.
Playfulness and number facts
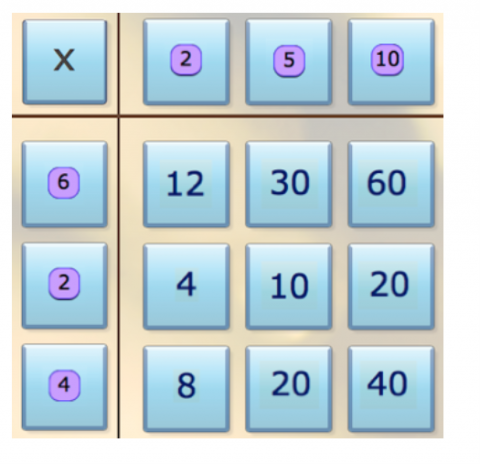
A really lovely way to encourage children to become more curious about mathematics involves reversing the nature of the task; 'working backwards' was a problem-solving strategy promoted by the prominent Hungarian mathematician George Pólya in his book 'How to solve it' (2004). Tables Teaser adopts this approach by presenting the answers to a set of multiplication calculations (using the 2, 5 and 10 times tables, up to 12x). In order to work out the row and column headings, learners may need to mentally run through many tables facts or many calculations, and select those which could be applicable. This playful task requires children to make connections, notice patterns and apply their knowledge in a way that completing a list of times tables questions does not do.
In conclusion
Playful activities can support learners develop their sense of factors and multiples in many different ways. They can explore interactivities, enjoy paired games and act out stories. Hopefully, their improving number sense will help prevent them and their families from making costly mistakes when they buy bicycles too!
References
Anghileri, J. (2000). Teaching number sense. London: A&C Black.
Dowker, A. (1992). Computational strategies of professional mathematicians. Journal for Research in Mathematics Education, 23(1), 45-55.
Polya, G. (2004). How to solve it: A new aspect of mathematical method (Vol. 85). Princeton University Press.
