PHIDDLYWINKS
What happens when you bring together Tiddlywinks and football?
You get Phiddlywinks!
Playing the game
Phiddlywinks is a game for two players. The winner is the first player to get the white counter into the coloured region at the opposite end of the board. Player 1 is aiming for the blue region and Player 2 for the red region.
The game begins with the white counter in the centre circle.
Players take it in turns to either:
- Place a black counter on the board or
- Move the white counter.
The white counter moves by jumping in a straight line over one or more black counters. A player may be able to make more than one jump when it is their turn.
To play Phiddlywinks, you can either print off black and white or colour versions of the board, or use the interactivity below.
Using the interactivity
To add a black counter, click on the point where you would like it to be placed.
To move the white counter, click on the black counter you want to jump over. When you have completed all your jumps, click on the 'Continue' button.
Clicking on the purple cog gives you the option to play against a friend, against the computer, or to watch two computers play against each other.
You may be interested in the article Phiddlywinks - a Tribute to John Conway, which gives a bit of background to this game.
Here are three different scenarios to consider:
Scenario 1: Player 1 to go next

Player 1 clicks on 7E (or 8F) and the white counter will move to 9G
Player 1 clicks on 9F (or 9E) and the white counter will move to 9D
Player 1 clicks on 9C and the white counter will move to 9B
Player 1 clicks on 10B and the white counter will move to 11B, winning the game!
Scenario 2: Player 2 to go next

Player 2's first move is to click on 5C, which will move the white counter to 4D
Player 2 now has two options for winning:
Either click on 3D (or 2D or 1D) and the white counter will move into the red region, winning the game
Or, click on 3C (or 2B) and the white counter will move to 1A, also winning the game.
Note that Player 2's second move cannot hop over the black counters at 3E, 2F and 1G to win, because the white counter would end up off the board.
Scenario 3: Player 1 to go next
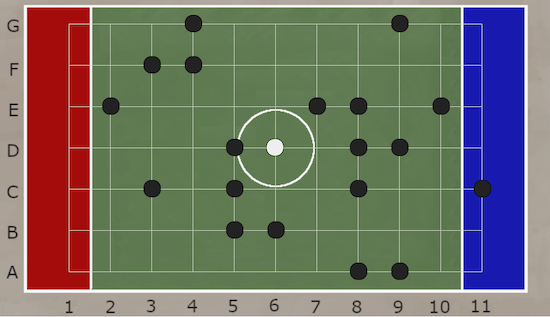
Player 1 clicks on 5C and the white counter will move to 4B
Player 1 clicks on 5B (or 6B) and the white counter will move to 7B
Player 1 clicks on 8C (or 9D or 10E) and the white counter will move to 11F, winning the game!
Why play this game?
The article Phiddlywinks - a Tribute to John Conway outlines the background to the creation of this game and the thinking that it prompts. This game could be introduced at the same time as students are learning about coordinates.
Introducing the game
Demonstrate the game using the interactivity, perhaps with the class playing against the computer intially (the default version). This could be followed up by discussing the three scenarios pictured below:
Scenario 1: Player 1 to go next

Player 1 clicks on 7E (or 8F) and the white counter will move to 9G
Player 1 clicks on 9F (or 9E) and the white counter will move to 9D
Player 1 clicks on 9C and the white counter will move to 9B
Player 1 clicks on 10B and the white counter will move to 11B, winning the game!
Scenario 2: Player 2 to go next

Player 2's first move is to click on 5C, which will move the white counter to 4D
Player 2 now has two options for winning:
Either click on 3D (or 2D or 1D) and the white counter will move into the red region, winning the game
Or, click on 3C (or 2B) and the white counter will move to 1A, also winning the game.
Note that Player 2's second move cannot hop over the black counters at 3E, 2F and 1G to win, because the white counter would end up off the board.
Scenario 3: Player 1 to go next

Player 1 clicks on 5C and the white counter will move to 4B
Player 1 clicks on 5B (or 6B) and the white counter will move to 7B
Player 1 clicks on 8C (or 9D or 10E) and the white counter will move to 11F, winning the game!
