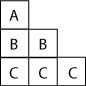
Alphabet BLOCKS
These alphabet bricks are painted in a special way. A is on one
brick, B on two bricks, and so on. How many bricks will be painted
by the time they have got to other letters of the alphabet?
Problem
A group of children painted letters of the alphabet on some cube bricks. They did it in a special way. They painted A on one brick, B on two bricks, C on three bricks, and so on.
Image

How many bricks had they painted by the time they had done the Cs?
How many bricks had they painted by the time they had done the Ds?
How many bricks had they painted by the time they had done the Es? And the Fs?
And the Gs?
And the Hs?
And the Is?
And the Js?
...
...?
Can you see why these totals are called triangle numbers?
Getting Started
What is the next letter of the alphabet?
How many bricks are needed for it?
How many bricks will that be altogether?
How many bricks are needed for it?
How many bricks will that be altogether?
Student Solutions
Thomas from Beechwood Park School didn't stop at the blocks with J on them:
C=6
D=10
E=15
F=21
G=28
H=36
I=45
J=55
K=66
L=78
M=91
N=105
O=120
P=136
Q=153
R=171
S=190
T=210
U=231
V=253
W=276
X=300
Y=325
Z=351
Chloe and Georgia from Moorgate CP School, and Matt from St Andrew's School also calculated carefully.
Class 5 from Spring Grove Primary School in Hounslow told us:
These numbers are called triangle numbers because you would be able to arrange the number of blocks into a triangle formation. It would also work if they were counters as well.
That's right! Thank you.
Teachers' Resources
Why do this problem?
This problem is an interesting way of practising addition and can be used to introduce children to the triangle numbers. It can also provide a context in which children can make mathematical predictions and justifications.Possible approach
You could begin by using, for example, multilink cubes to represent the blocks. Show the children a red one and say that you could write an "A" on it. Then take two blue ones to write "B" on, then three yellows for "C". Ask the children how many blocks you have used altogether. How many would you have with the "D"s as well? How do they know? You could encourage them to talk to a partner and
use a mini-whiteboard or paper to jot down ideas. You can then set them off to work on the rest of the task.
You could use a plenary to talk about the different ways the children have worked on the problem - for example sharing different ways of recording. You might want to make a list of the totals on the board (1, 3, 6, 10, 15 etc) and ask the class whether they can see why these are triangle numbers. You could refer to square numbers to get them thinking, or draw patterns on the board.
Key questions
What is the next letter of the alphabet?
How many bricks are needed for it?
How many bricks will that be altogether?
Possible extension
You could ask some children to predict how many blocks will have been used once, for example, the letter N has been used. How do they know? How about for the whole alphabet? Do they have any quick ways of working this out?
Possible support
Using cubes to represent the blocks will help all children get started on this problem. When it comes to finding out why they are called triangle numbers, you could suggest that learners use squared paper and put the letters in the squares, for example:
Start like this:
Image