Thousands of people
How many thousand people does each dot represent?
Problem
In the land of Mathia, there are six towns, Algeby, Bracketon, Costown, Divisham, Ethorpe and Factorbridge. They are shown on the map below:
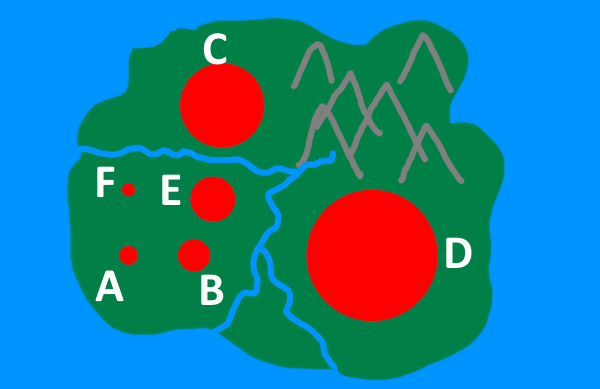
Algeby has 1000 inhabitants.
If each circle on the map represents the population of the town, can you estimate the population of the other five towns?
Once you've had a go at estimating, click below to read on.
If we choose units so that A has a radius of 1, then the radius of each circle is shown in the table below:
Assuming the population of each town is proportional to the area of each circle, can you work out the actual populations of towns B, C, D, E and F?
Sometimes, when presenting data in this way, someone might choose to make the radius proportional to the population rather than the area. Compare your estimates to the actual populations, and to what the populations would be if the diagram used radius instead of area.
Which do you think is a better choice for representing the data - radius, or area?
When representing data, it is good practice to make sure the areas of regions used to convey numerical data are in proportion with the size of the number being represented.
Have a look in a newspaper or online for charts, diagrams and infographics where figures are misrepresented by using uneven scales, angled three-dimensional pie charts, or other representations that distort area. Why might someone choose to represent their data in this way?
You might like to try Where Are You Flying? next.
This resource is part of the collection Statistics - Maths of Real Life
Image

Algeby has 1000 inhabitants.
If each circle on the map represents the population of the town, can you estimate the population of the other five towns?
Once you've had a go at estimating, click below to read on.
If we choose units so that A has a radius of 1, then the radius of each circle is shown in the table below:
| Town | Radius |
|---|---|
| A | 1 |
| B | 1.7 |
| C | 4.5 |
| D | 7 |
| E | 2.4 |
| F | 0.7 |
Assuming the population of each town is proportional to the area of each circle, can you work out the actual populations of towns B, C, D, E and F?
Sometimes, when presenting data in this way, someone might choose to make the radius proportional to the population rather than the area. Compare your estimates to the actual populations, and to what the populations would be if the diagram used radius instead of area.
Which do you think is a better choice for representing the data - radius, or area?
When representing data, it is good practice to make sure the areas of regions used to convey numerical data are in proportion with the size of the number being represented.
Have a look in a newspaper or online for charts, diagrams and infographics where figures are misrepresented by using uneven scales, angled three-dimensional pie charts, or other representations that distort area. Why might someone choose to represent their data in this way?
You might like to try Where Are You Flying? next.
This resource is part of the collection Statistics - Maths of Real Life
Student Solutions
| Town | Radius | Area | Population (nearest hundred) |
|---|---|---|---|
| A | 1 | $\pi$ | 1000 |
| B | 1.7 | $2.89 \pi$ | 2900 |
| C | 4.5 | $20.25 \pi$ | 20000 |
| D | 7 | $49 \pi$ | 49000 |
| E | 2.4 | $5.76 \pi$ | 5800 |
| F | 0.7 | $0.49 \pi$ | 500 |
If the diagram represented the populations using radius rather than area, the populations would be as follows:
A 1000
B 1700
C 4500
D 7000
E 2400
F 700
Most people's estimates should match more closely to the area figures than the radius ones.
Teachers' Resources
Why do this problem?
This problem gives students the opportunity to investigate the way area distortions can be used to present data in a misleading fashion.Possible approach
Show the map:
Image

"If Town A has 1000 inhabitants, and a larger circle means more people live there, can you estimate the populations of the other towns?"
You may wish to give students a cop of the map. Once they have written down their estimates, share with them the table showing the radius of each circle:
| Town | Radius |
|---|---|
| A | 1 |
| B | 1.7 |
| C | 4.5 |
| D | 7 |
| E | 2.4 |
| F | 0.7 |
"If the number of inhabitants is proportional to the area of each circle, can you work out the population of each town?"
Give students some time to perform the calculations in groups. Then bring the class together and discuss whether their estimates assumed proportionality to the area or the radius. Finally, share examples of data presentations where areas are distorted to skew perceptions of the data, and discuss why people might choose to present data in this way.
Key questions
Which is a better choice for representing relative proportions - radius (length) or area?Why might people deliberately choose to represent data in a less transparent way?
