Proofs with Pictures
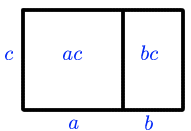
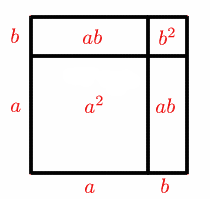
The algebraic identities $(a+b)c \equiv a c + b c$ and $(a+b)^2 \equiv a^2 + 2a b + b^2$ can be justified by pictures, as Figures 1 and 2 show.
Image
|
Image
|
|
| Figure 1 | Figure 2 |
Arguments of this nature can be found in Euclid's The Elements (book II) . Like Euclid, we will assume throughout this discussion that $a$, $b$ and $c$ are non-negative.
Inequalities can also be demonstrated by pictures. For example, the inequality $(a+b)^2 \ge a^2 + b^2$ is shown by figure 2.
Image
|
| Figure:3 |
In figure 3, two rectangles, each of area $a b$, fit inside the two squares of areas $a^2$ and $b^2$, showing that $a^2 + b^2 \ge 2a b$.
In the April 2000 issue of Mathematics Magazine , Claudia Alsina gives further examples of inequalities which can be proved by pictures.
In the April 2000 issue of Mathematics Magazine , Claudia Alsina gives further examples of inequalities which can be proved by pictures.
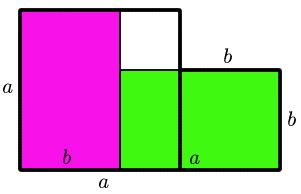
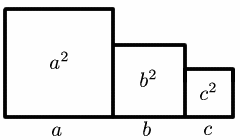
Figures 4 and 5 demonstrate the inequality $a^2 + b^2+ c^2 \ge a b + b c + c a$.
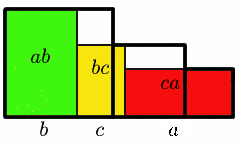
In Figure 4, three squares of areas $a^2$, $b^2$ and $c^2$ are shown, assuming (without loss of generality) that $a \ge b \ge c$.
Image
|
Image
|
|
| Figure 4 | Figure 5 |
In Figure 5, three rectangles of areas $a b$, $b c$ and $c a$ are fitted inside the three squares, showing that $a^2 + b^2 + c^2 \ge a b + b c + c a$.
Using this inequality, then from Figures 6 and 7 the inequality $a^3 + b^3 + c^3 \ge 3a b c$ can be demonstrated.
Image
|
Image
|
|
| Figure 6 | Figure 7 |
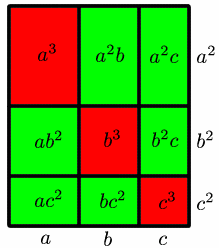
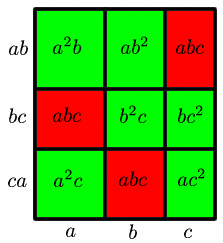
The two rectangles have the same base length $a + b + c$, but the rectangle in Figure 6 has height $a^2 + b^2 + c^2$, which as we have seen is greater than the height $a b + b c + c a$ of the rectangle in Figure 7. So the area of the rectangle in Figure 6 is greater than the area of the rectangle in Figure 7.
The two rectangles are each divided into nine small rectangles, with areas as shown. The six green rectangles in Figure 6 have the same areas as the six green rectangles in Figure 7 ($a^2b$, $b^2c$, $a^2c$, $a b^2$, $b c^2$, $a c^2$). Comparing the remaining areas shows that $a^3 + b^3 + c^3 \ge 3a b c$, as required.
The AM-GM inequality
The inequalities $a^2 + b^2 \ge 2a b$ and $a^3 + b^3 + c^3 \ge 3a b c$ can be written in the form\begin{eqnarray} \\ \frac{x_{1} + x_{2}}{2} & \ge & (x_{1}x_{2})^{1/2} \\ \frac{x_{1} + x_{2} + x_{3}}{3} & \ge & (x_{1}x_{2}x_{3})^{1/3} \end{eqnarray}
where \[ x_{1} \ge 0, x_{2} \ge 0, x_{3} \ge 0. \]
These are special cases of the important Arithmetic Mean - Geometric Mean inequality (the AM-GM inequality)
\begin{eqnarray} \frac{x_{1} + x_{2} + \ldots x_{n}}{n} \ge (x_{1}x_{2}\ldots x_{n})^{(1/n)}, \end{eqnarray}
where
$x_{i} \ge 0, 1 \ge i \ge n $
When is an inequality an equality?
When an inequality is established, it is always important to know under what circumstances equality can occur.
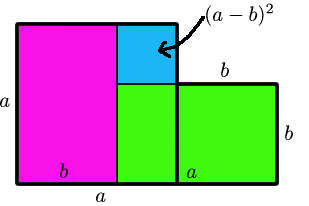
A re-examination of Figure 3 (see Figure 8) shows that the inequality $a^2 + b^2 \ge 2a b$ becomes an equality if and only if the blue region has zero area.
Image
|
| Figure: 8 |
The blue region is a square of area $(a-b)^2$, which is zero if and only if $a = b$.
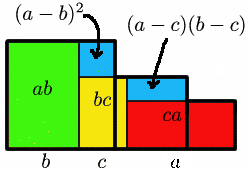
Similarly, a re-examination of Figure 5 (see Figure 9) shows that the inequality \[ a^2 + b^2 + c^2 \ge a b + b c + c a \]
is an equality if and only if the two blue regions have zero area.
Image
|
| Figure: 9 |
This occurs if and only if $(a-b)^2=(a-c)(b-c)=0,$
i.e. if $a=b=c$
It follows that the inequality $a^3 + b^3 + c^3 \ge 3a b c$ is an equality if and only if $a = b = c$.
(Remember that throughout this discussion it was assumed that $a\ge0$, $b\ge0$ and $c\ge0$. It can in fact be proved that $a^3 + b^3 + c^3 \ge 3a b c$ under the weaker assumption that $a+b+c\ge 0$, and that equality holds if and only if $a+b+c=0$. How? Just look hard at the factorisation $$ a^3+b^3+c^3-3a b c = (a+b+c)(a^2+b^2+c^2-a b-b c-c a) $$
