Polar Coordinates
If you have learnt about coordinate geometry at school, then the coordinate system you used was probably the Cartesian one. The Cartesian system describes the location of each point $p$ in the plane by two coordinates $(x,y)$. To find $p$ you start at the point $(0,0)$ and walk a distance $x$ parallel to the horizontal axis and a distance $y$ parallel to the vertical axis.
We take Cartesian coordinate system for granted these days, but when it first became popular 17th century (in part due to the mathematician René Descartes after whom it is named) it was nothing short of a revolution. For the first time in history it enabled people to describe geometric shapes by equations. For example, The equation $$y=2x+1$$ describes a straight line, the equation $$y=x^2$$ describes a parabola, and the equation $$x^2+y^2=4$$ describes a circle.
Can all geometric shapes be described so easily, using comparatively simple equations? Consider the spiral shown in the picture below. It's an example of an Archimedean spiral and is characterised by the fact that the turns of the spiral are evenly spaced.
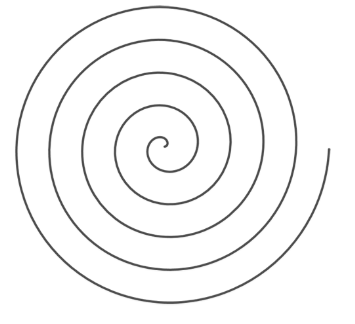
It's far from obvious how to describe this spiral using Cartesian coordinates. There is a formula that does this, but it is not pretty - you can see it below.
But never fear - something amazing happens when you exchange Cartesian coordinates for polar coordinates. Instead of describing the location of each point $p$ in the plane by an $x$-coordinate and a $y$ coordinate, the polar system uses a coordinate called $r$ and a coordinate called $\theta$. The coordinate $r$ is the distance from $(0,0)$ to $p$ along a straight radial line, and $\theta$ is the angle formed by that radial line and the positive $x$-axis, measured anti-clockwise from the $x$-axis to the line.
In the image below, click on the point and drag it around to see how its polar coordinates $(r,\theta)$ change (degrees are measured in radians).
In polar coordinates the Archimedean spiral above is described by an equation that couldn't be simpler:
$$r=\theta.$$
In other words, the spiral consists of all the points whose polar coordinates $(r,\theta)$ satisfy this equation. The animation below shows the ray corresponding to the angle $\theta$ as $\theta$ ranges from $0$ to $2\pi$. The point $p$ marked on the ray is the one with coordinates $(\theta, \theta)$. (Click on the play icon in the bottom left hand corner or use the slider to vary $\theta$.)
This is the beginning of our spiral. To get the rest keep turning the radial line by more than one full turn, through one-and-a-half turns ($3\pi$), two turns ($4\pi$), and so on, round and round. In the animation below $\theta$ runs from $0$ to $10\pi$.
In general Archimedean spirals are described by equations of the form
$$r=a\theta$$
for $a$ a positive real number. By playing around with different values for $a$ you can convince yourself that $a$ controls how tightly the spiral is wound up.
If you prefer a physical interpretation of your geometric shapes, an Archimedean spiral is what you get when you trace the path of a point that moves out from the centre at constant speed along a line that rotates with constant angular velocity.
Another famous family of spirals consists of the logarithmic spirals, whose polar coordinates are given by equations of the form
$$r=a e^{b\theta}$$
Where $a$ and $b$ are positive real numbers and $e$ is the base of the natural logarithm. The picture below shows a logarithmic spiral with $a=1$ and $b=\tfrac{1}{10}$.
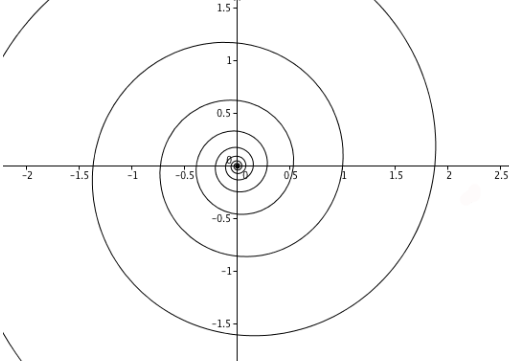
Logarithmic spirals are famous because they often occur in nature. You can see them in the turns of a snail shell, in many plants and even in the arms of spiral galaxies. The 17th century mathematician Jacob Bernoulli was so fascinated by this beautiful shape, he called it the "spiral mirabilis" (miraculous spiral) and asked for it to be engraved on his tombstone. Unfortunately the engravers got it wrong and he ended up with an Archimedean spiral on his grave instead. You can read more about logarithmic spirals, as well as other beautiful shapes described in polar coordinates, in the Plus magazine article Polar power.
So which coordinate system is best, the polar one or the Cartesian one? It depends on what you are trying to do. Some shapes work better in the Cartesian system and some in the polar system. The important thing is that a change from one system to the other can turn gruesome equations into beautifully simple ones. If in doubt explore both options!
You may wish to have a go at the problem Polar Bearings to explore different curves and their representations in Cartesian and Polar Coordinates.
Cartesian equation for the Archimedean spiral
In Cartesian coordinates the Archimedean spiral above is described by the equation
$$y=x tan(\sqrt{x^2+y^2}).$$
