Sticky Dice
Problem
Throughout these challenges, the touching faces of any adjacent dice must have the same number.

In the picture above, three dice are joined with 4s between the blue and green, and therefore 3s between the green and red.
The total of the numbers on the top is 9 in each case.
The two arrangements will be thought of as the same even though they are in a different order and colour. This is true for all the challenges.
For the challenges below, you'll be using four dice.
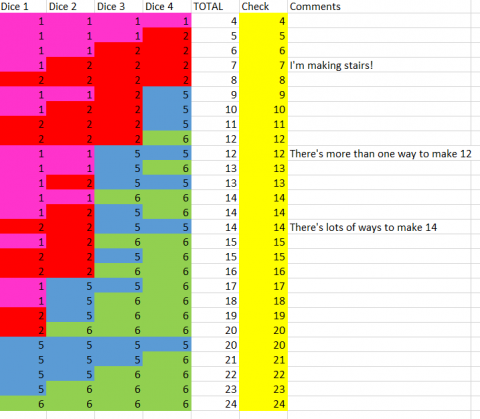
Challenge 1
Find a way of making the total on the top come to each number from 11 to 18 inclusive, keeping to the same joining numbers throughout.
Here is an example:

Remember, any touching faces must be a pair of the same numbers.
Challenge 2
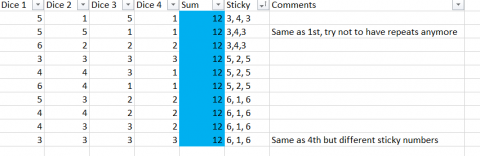
Using any joining numbers, find as many different ways as possible to make the tops add up to 12.
How can you be sure you've found all the possible ways?
Challenge 3
Arrange the dice in as many ways as possible, so the total of the tops of the left-hand pair is twice the total of the tops of the right-hand pair.
In the picture below, the top total of the left-hand pair is three times the right-hand pair, not two times so you cannot use this arrangement.

Challenge 4
Arrange the dice in as many ways as possible, so the pair on the left-hand side has a top product* which is double or treble the right-hand pair product.
In the picture above, the left-hand pair product is twelve times bigger than the right.
*The product of two numbers is one multiplied by the other. For example, the product of 3 and 5 is 15 because 3x5=15.
Here is a sheet of the activity.
Student Solutions
You've successfully completed Challenge 1 by finding a way of making each number, but I think there are a few more ways of making some of these numbers if you would like to find all of the possibilities.
| Sticky numbers | Numbers I can use | How to make 12 |
|---|---|---|
| 1, 6, 1 | 5, 4, 3, 2 |
5, 3, 2, 2 |
| 2, 5, 2 | 6, 4, 3, 1 |
6, 4, 1, 1 |
| 3, 4, 3 | 6, 5, 2, 1 |
6, 2, 2, 2 |
Well done for working systematically, Alba! You're right, these are the nine different ways of making 12.
| Sticky numbers | Numbers I can use | Possible ways |
|---|---|---|
| 1, 6, 1 | 5, 4, 3, 2 |
5, 4, 2, 3 (this is the only solution in this table that is incorrect - can you see what Alba might have meant to type?) |
| 2, 5, 2 | 6, 4, 3, 1 |
6, 6, 3, 3 |
| 3, 4, 3 | 6, 5, 2, 1 |
6, 6, 5, 1 |
Teachers' Resources
Why do this problem?
This task allows all pupils to have a positive experience of solving problems, as it requires very little mathematical knowledge. It encourages a systematic approach and provides an opportunity for pupils to explain how they know they have all the solutions.Possible approach
As a class, begin with three large dice. Discuss what the first instruction means - what are 'the touching faces of adjacent dice'? Ask a pupil to demonstrate how to 'stick' the three dice together.Once the dice are 'stuck' together, discuss what the total of the numbers on the top is. If we switched the numbers around as in the first picture, would this be the same arrangement or a different arrangement? Encourage pupils to discuss their ideas, and then explain that for this activity we will be thinking of both arrangements as being the same.
Once pupils have understood these key ideas, give them time to work in small groups on the four challenges.
Key questions
Explain what you are doing to find the next arrangement.Tell me how you are recording your results.
Will you know if you have found them all? How?