A Curious Collection of Bridges
Here is a puzzle. The map below shows a city divided by a river, which contains two islands with seven bridges linking the various pieces of land masses. Can you find a walk through the city that crosses every bridge exactly once? And if not, can you show that there isn't one?
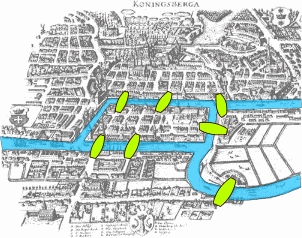
Can you find a path that crosses every bridge once and only once?
It's a puzzle that's hard to resist. The map of the bridges and the river is so simple, many people feel compelled to find a pen and begin tracing out possible routes, and seeing where they get stuck. If you're also overcome by this desire to experiment, then you're in good company: this very puzzle inspired the great 18th century mathematician Leonhard Euler to develop a whole new area of maths.
The puzzle originated in the Prussian city of Königsberg (now Kaliningrad), shown in the map above as it was in 1652. The river is the River Pregel. Many citizens of Königsberg tried to find the winning route on foot; many even claimed they found it, but nobody could ever reproduce their answers. In 1736 Euler explained why: he showed that such a walk didn't exist.
Euler's solution is surprisingly simple once you look at the problem in the right way. The trick is to get rid of all unnecessary information. It doesn't matter what path the walk takes on the various land masses. It doesn't matter what shape the land masses are, or what shape the river is, or what shape the bridges are. So you might as well represent each land mass by a dot and a bridge by a line. You don't have to be geographically accurate at all: as long as you don't disturb the connectivity of the dots, which is connected to which, you can distort your picture in any way you like without changing the problem.

(The middle 7 bridges image was created by Xiong, Nux and Chris-martin and is reproduced under a Creative Commons license. The other two images are in the public domain.)
Once you have represented the problem in this way, its features are much easier to see. After playing around with it for a while you might notice the following: when you arrive at a dot via a line (that is, you enter a land mass via the bridge), then unless it is the final dot at which your walk ends, you need to leave it again, by a different line, as those are the rules of the game. That is, any dot that is not the starting and end-point of your walk needs to have an even number of lines coming out of it: for every line along which you enter there has to be one to leave.
For a walk that crosses every line exactly once to be possible, at most two dots can have an odd number of lines coming out of them. In fact there have to be either two odd dots or none at all. In the former case the two correspond to the starting and end points of the walk and in the latter the starting and end points are the same on any walk. In the Königsberg problem, however, all dots have an odd number of lines coming out of them, so a walk that crosses every bridge is impossible.
Euler's solution also laid the foundation for an area of maths that couldn't be more relevant to modern life: network theory. A network (also known as a graph) is a collection of nodes connected up by links (in the bridges problem the nodes would represent the bits of land and the links between them the connecting bridges). Networks are absolutely everywhere. We live in social networks, travel along road and rail networks, and rely on telephone networks and utility networks that deliver power or water. Our computers and phones are hooked up to that vast network called the internet; rivalled in complexity only by the network of neurons in our brains, which enables us to produce all these complex structures in the first place.
If you want to test how well you have understood this article, you might like to try the problem Can You Traverse It?
You can find out more about Graphs and Networks on our sister site Plus.
