Candles
What is the ratio of the lengths of the candles?
Problem
Two candles have different lengths and different thicknesses. The shorter one would last 11 hours, the longer one would last for 7 hours.
Both candles are lit at the same time, and 3 hours later both have the same length remaining.
What was the ratio of the length of the longer candle to the shorter candle?
This problem is taken from the World Mathematics Championships
Student Solutions
Answer: 11:14
Using an area model
Let the height represent the height and the area the time left, so width is thickness (or other variable that affects the rate of the burning of the candle).

After 3 hours, 8 hours left and 4 hours left
$\therefore$ width of shorter candle is $2\times$ width of longer candle

$\therefore$ 3 hours on the short candle has the same height as 1.5 hours on the long candle
$\therefore$ heights are in the ratio (4 + 1.5) : (4 + 1.5 + 1.5)
5.5 : 7
11 : 14
Using rates
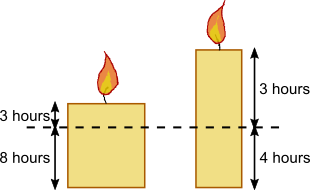
After 3 hours, both candles are the same length.
This will burn for 8 hours on the shorter candle and 4 hours on the longer candle.
$\therefore$ the longer candle burns twice as fast as the shorter candle.
So if the longer candle were as fat (or whatever other property affects burning time) as the shorter candle, it would burn for 7$\times$2 = 14 hours.
So their lengths are in the ratio 14 : 11.
Using fractions
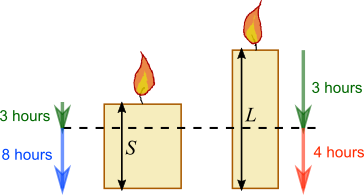
After 3 hours:
shorter candle length is $\frac8{11}S$
longer candle length is $\frac47L$
So $\frac8{11}S=\frac47L\Rightarrow7\times8\times S=11\times4\times L\Rightarrow14\times S=11\times L$.
This means the ratio $L:S$ is $14:11$.
(This follows because if $L=14k$ and $S=11k$, then $14\times S=14\times11k$ and $11\times L=11\times14k$, which are equal).
