Alison's Quilt
Nine squares are fitted together to form a rectangle. Can you find its dimensions?
Problem
Alison's Quilt printable sheet

Alison joins together nine squares with side lengths $1, 4, 7, 8, 9, 10, 14, 15$ and $18$ cm with no gaps and no overlaps, to form a rectangular quilt.
Can you find the dimensions of the finished quilt, and show how Alison fitted the squares together?
Alison wants to make a second quilt from ten squares with side lengths $3, 5, 6, 11, 17, 19, 22, 23, 24$ and $25$ cm.
Can you find the dimensions of this quilt?
Getting Started
If you work out the areas of the squares you can deduce the area of the rectangle...
Student Solutions
Nikki and Mollie from Holy Trinity CE Academy, Rothwell cut out squares with the side lengths from the problem and moved them around until they fitted togther to make a quilt. Elliot, Ted and Callum from Priestlands School and Janani and Deniz from Nonsuch High School for Girls also worked it out by fitting the squares together. Janani and Deniz started with the largest square (18 cm) and then found other combinations of squares that could go next to it.
Naomi from North London Collegiate School used the idea that the smaller squares must line up along the sides of the larger squares perfectly, so their lengths will need to match:
1. Since the size of two quilts would add up together to make up to one side of the quilt, you must find all of the possible sums for each number using other numbers in the collection (see fig 1).
2. After I came up with all the possible sums for each number, I condluded that I should have 7, 8, 9 on the side of 1. So I started the quilt with 1 in the middle (see fig. 2).
3. 1 + 7 = 8. So I would put 8 on top of the 1 and 7. I continued doing so until I used up all of the squares (see fig.3)
4. Therefore, after the quilt was finished, I worked out the area by doing $a\times b$ (see fig. 3) which, in this case, is $(9+8+15)\times(15+18)=32\times33=1056$ cm$^2$.
Matt from Swindon Academy in the UK, Lavya from MGIS in India, class 8e1 from Ousedale in the UK, Laila, Lucy and Alice from Holy Trinity CE Academy, Rothwell in the UK and Gaia from Gess Singapore began by finding the area of the quilt. 8e1 said:
To start with, for the first quilt, we worked out the area of the rectangle which was each of the squares' side lengths, squared and added together. This came to 1056. We then worked out the factors of 1056 to find the dimensions of the rectangle and the only possible lengths were 22cm and 48cm, 24cm and 44cm and 32cm and 33cm. This was because each length had to be over 18cm.
Lavya, Matt and 8e1 tried putting the larger squares around the outside. This is 8e1's working:
We then eliminated 22 and 48 as it wouldn't work, this was because if you put the smaller squares on the outside lengths then you wouldn't have the right sized squares to fill in all the gaps. For example, if you put the 4 next to the 18 to make 22 then you wouldn't have any more small squares to fill the space. We also found this to be true for 24 and 44. Therefore, we knew the dimensions had to be 33 and 32 and also that the larger squares had to be on the outside. We then made the squares and used this knowledge to make half of the rectangle and then filled in the gaps with the remaining shapes.

Having found the side lengths of the quilt, Gaia worked out which squares could go next to each other to make those lengths:
Out of my lengths squares sides (1,4,7,8,9,10,14,15 & 18) which is the easiest sum combination that can give me 32 and 33?
I considered that the small square of 1 cm for sure will be somewhere in the middle, otherwise I can't build up a rectangle and most probably also the 4 cm one will stay in the middle, so for now I don't consider these 2 squares.
The easiest sum to get to 33 is 18+15.
The other side of 32 cm needs to have one side of a smaller square in common, so on one side I have to reach 32, starting from 18 cm (32$-$18=14), on the opposite side I have to reach 32, starting from 15 cm (32$-$15=17).
I have available a square of 14 cm, but not one with a side of 17 cm.
With the error and trial method, I considered the possible combinations of 17 (10+7 or 8+9) and tried to build up the rectangle.
Lavya, Matt and 8e1 also made the second quilt. This is Matt's working:
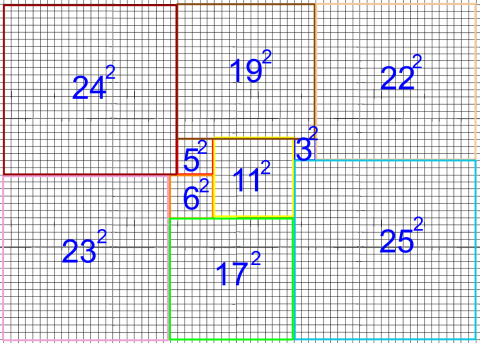
Thank you also to Martha from Wycombe High School in the UK, who sent in a correct image of the first quilt.
Teachers' Resources
Why do this problem?
In this problem students can work on both prime factorisation and area of rectangles.
Possible approach
Pose the first problem:
"Alison joins together nine squares with side lengths $1, 4, 7, 8, 9, 10, 14, 15$ and $18$ cm with no gaps and no overlaps, to form a rectangular quilt.
Can you find the dimensions of the finished quilt, and show how Alison fitted the squares together?"
Invite students to think on their own, then discuss in pairs how they might tackle the problem, and then share strategies in a class discussion.
Key questions
What must the area of the finished quilt be?
How do you know?
What can you say about rectangles with that area?
What are the possible dimensions of the quilt?
Encourage students to test out different possible arrangements by sketching how the squares might fit into their proposed rectangle.
Once students have successfully found the first rectangle, challenge them with the second task:
"Alison wants to make a second quilt from ten squares with side lengths $3, 5, 6, 11, 17, 19, 22, 23, 24$ and $25$ cm. Can you find the dimensions of this quilt?"
Possible support
You may wish to provide squared paper for students who want to make the nine squares and assemble them.
Possible extension
Dissecting squares and rectangles into smaller pieces is a very fruitful area for investigation. The problems Dissect and Building Gnomons might be of interest.
