Dissect
What is the minimum number of squares a 13 by 13 square can be dissected into?
Age
11 to 14
Challenge level
Problem
It is possible to dissect any square drawn on a grid into smaller squares, by cutting along grid lines.
Image
For example a 3 by 3 square can be dissected into either 9 smaller squares or 6 squares:
- What is the minimum number of squares a 13 by 13 square can be dissected into?
- What is the smallest size square which can be dissected into squares which are all different sizes?
Student Solutions
The minimum number of squares a 13 by 13 square can be dissected into is 11: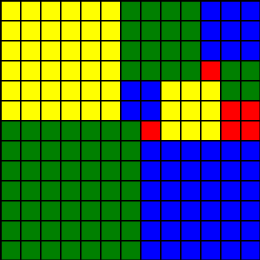
Image
There is one trivial solution to the size of the smallest square which can be dissected into squares which are all different sizes: the unit square! The smallest non-unit square which can be dissected into squares which are all different sizes has sides of length 175 units.
For further information on this and other similar problems see Chapter 11, Mrs. Perkins Quilt and Other Square-Packing Problems in Mathematical Carnival by Martin Gardner, published by Pelican books.
Teachers' Resources
It is certainly worthwhile looking at gradually increasing the size of the squares. With younger pupils it would be good to allow them to discuss the situation for even sided squares and those with a side that is a multiple of 3. For older/more able pupils its a good idea to go at least as far as a 43 by 43 square! When a large number have been tried I would suggest that pupils try to examine their "system" for getting the least number of squares.