Frogs
How many moves does it take to swap over some red and blue frogs? Do you have a method?
Problem
Watch the video for an introduction, or scroll down to have a go.
If you can't see the video, reveal the hidden text which summarises the video
Imagine two red frogs and two blue frogs sitting on lily pads, with a spare lily pad in between them.

Frogs can slide onto adjacent lily pads or jump over a frog; frogs can't jump over more than one frog.
Can you swap the red frogs with the blue frogs?
What is the minimum number of moves you need to swap them over?
Experiment with different numbers of red and blue frogs.
Can you always swap the frogs over without having to move any frogs backwards?
Can you swap the frogs over when the number of red and blue frogs is not the same?
You can use the interactive environment below or explore with counters.
Full Screen and tablet version
Can you see any patterns in the sequence of moves that it takes to swap the frogs over?
Can you explain why those patterns occur?
Can you predict the minimum number of moves it will take for any number of red and blue frogs?
Can you describe a method for swapping all the frogs over in the minimum number of moves?
Printable NRICH Roadshow resource.
Getting Started
Keep a record of the number of jumps and the number of slides.
Try increasing the number of frogs on each side by one at a time. What patterns can you see?
Student Solutions
Rohan from Wilson’s School in England and Sowjanya, Avyukt, Taran, VinamaraSai, Niveditha, Adhrit, Sara, Achyuth, Abheer, Kavicharan, Agasthya, Pranit, Riddhit and Eshaan (with Shubhangee) from Ganit Kreeda, Vicharvatika in India investigated the number of moves needed when there are the same number of red and blue frogs. Shubhangee wrote:
We explored to find minimum number of moves to swap with different number of frogs using interactivity. Strategy we used to swap pink frogs (on left) with blue frogs (on right) in minimum number of moves without moving backward was:
- No same coloured frog will come back to back.
- Always create a gap between two same coloured frogs, so that the other coloured frog can jump/ slide to fill the gap.
Rohan added some more advice:
From experimenting with red and blue frogs, I concluded that you could always swap the frogs over without moving any frogs backwards. The key thing to remember was that an alternating pattern of red and blue frogs should be maintained whilst moving the frogs.
Shubhangee’s students then recorded the minimum number of moves in a table. These are Niveditha’s recordings:
Here are Agastya and Pranit’s observations:
Here are Taran’s recordings:
Rohan continued this approach:
I realised that the change in moves were all odd numbers and increased in increments of 2. From this, I could create a formula to predict the number of moves required using n as the number of blue or red frogs (since, in this instance, they are equal): No. of moves $= n^2 + 2n$
VinamaraSai, Adhrit and Avyukt’s recorded the moves:
Moves recorded as Pink(P) and Blue(B) Frogs:
P
BB
PPP
BBB
PPP
BB
P
Ci Hui Minh Ngoc Ong from Kelvin Grove State College (Brisbane) in Australia and Sowjanya, Sara and Achyuth used S to represent a Swipe and H to represent a Hop. This is Sowjanya, Sara and Achyuth’s work which begins by using four frogs of each colour.
It can be further generalized for $n\times n$ frogs as:
No. of moves $= 1+2+3+---+n+n+n+---+3+2+1$
No. of moves $= \frac{n(n+1)}{2} + n + \frac{n(n+1)}{2}$
No. of moves $= n(n+1) + n$
No. of moves = $n^2 + 2n = n(n+2)$
Can you see how all the formulas above mean the same thing?
Daya from Hutchesons’ Grammar School in the UK, Yu-Tong from Colyton Grammar School in England, Rohan and Ci Hui Minh Ngoc Ong experimented with different numbers of red and blue frogs. Daya and Ci Hui Minh Ngoc started with just one frog of one colour. Daya wrote:
I found a pattern between numbers with having a certain amount of frogs on 1 side and just one frog on the other side. I went up by one each time, so I started with 1,1 and got 3 moves, each time I added another number to the left side the amount of moves increased by 2. When I did 2,1 I got 5 moves and they kept on increasing by 2 each time.
This is Ci Hui Minh Ngoc Ong’s work (click to enlarge):
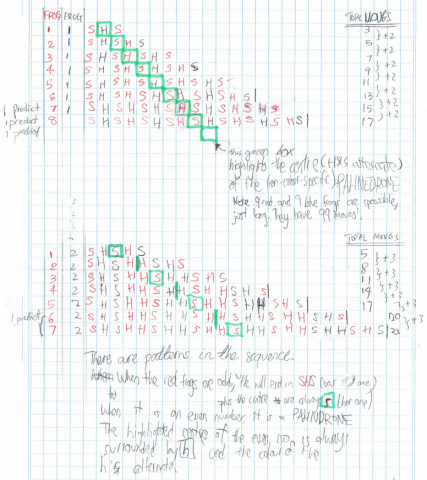
Rohan tried using one more frog of one colour than the other, and then two more, and so on:

Yu-Tong found the same formula, but wrote it in a different and more general way:
The number of red frogs multiply by the number of blue frogs equals the number of jumps and if you add the number of the two different coloured frogs it will equal the number of slides so the formula would be rb+r+b to get the number of moves if r represents the number of red frogs and b represents the number of blue frogs.
Yu-Tong’s method is below, but thnk about why the number of jumps is equal to $b\times r$, and why the number of slides is equal to $b+r$ - or one slide per frog. If you are already convinced that the frogs can always move into their final position without going backwards, is this enough to convince you that this forumla must be correct?
Yu-Tong’s method:
At first I used 2 red frogs and 2 blue frogs and the number of moves were 8 and 3 frogs of each colour and got 15. I noticed that 2 red frogs multiplied by 2 blue frogs then doubled would get 8. However this did not work for 3 red and 3 blue frogs so I tried to but it in another way. I found that another way was 2(2+2) and this would also give the answer 8 so I tried the method of 3 red and 3 blue frogs and it got me the answer 15. After many tries I came to a conclusion that with the same number of frogs on each side the method{2(2+2) = a(a+a)} works so then I tried it on an occasion when the number of frogs aren't the same.
When I tried 2 red frogs and 3 blue frogs I found out that either way it would be one less or one too more. From this I figure out that this equation a(a+a) is the same as a*a+a+a and if the numbers are different then it would be a*b+a+b. The main methods used was first looking for a pattern that I wrote it in algebra and then expanded it to get the solution.
Teachers' Resources
Why do this problem?
This problem requires students to visualise, work systematically, and develop good representations. The engaging nature of the problem encourages students to persevere in order to get to a solution. Along the way they will notice patterns, make conjectures, and perceive structure to explain the patterns they notice.
Possible approach
This problem featured in the NRICH Primary and Secondary webinar in September 2022.
Demonstrate the problem to the class. One way is to seat 4 students on 5 chairs, two wearing red hats/scarves/jumpers and two wearing blue, and act the problem out.
Give the class some time to play with the problem, using counters or the interactivity. If students are using counters, they may find this Game Board and Recording Sheet useful.
Full Screen and tablet version
Then bring the class together to share any initial noticings, and perhaps to demonstrate 3 red and 3 blue frogs, for example.
The interactive allows you to enter students' names after they have finished swapping the frogs, and these can be saved and replayed.
Next, set the challenge:
"In a while, I am going to choose a number of red and blue frogs, and challenge you to swap them over using as few moves as possible and be able to predict before you start how many moves it will take you."
Give the class some time to start thinking about the problem. When appropriate bring them together to move their thinking on:
"It may be helpful to look for patterns in the sequence of moves that it takes to swap the frogs over. You might find it easier to see those patterns if you have a good recording system."
While students are working, look for examples of clear thinking, explanations and recording strategies, ready to share these with the rest of the class.
Here are some possible methods students might employ - you may wish to suggest some of them to students who are struggling to express their thinking clearly on paper:


Bring the class together to share what they have found. Invite a few students to share their insights and any recording strategies that helped them.
Finally, use the interactive environment to perform a frog swap with, say, 7 red frogs and 6 blue frogs. You could invite one pair of students to start off, and then stop them part way through and ask another pair to take over.
Key questions
How do you know whether you need to jump next, or slide next?
How many places will the frogs have moved by the end?
How many jumps will there be altogether?
Can you explain the patterns you notice?
Possible support
Restrict the problem to exploring the number of moves when there are the same number of frogs on each side. Encourage students to record the number of jumps and the number of slides.
Possible extension
Without looking at the screen or your counters, and without drawing any diagrams, can you write out a sequence of moves to swap over some red frogs and blue frogs?
One approach might be to fix the number of blue frogs and explore what happens as you increase the number of red frogs.
