More Isometric Areas
Isometric Areas explored areas of parallelograms in triangular units. Here we explore areas of triangles...
Problem
This problem follows on from Isometric Areas.
More Isometric Areas printable sheet
Printable isometric paper
Here is an equilateral triangle with sides of length 1.
Let's define a unit of area, $T$, such that the triangle has area $1T$.

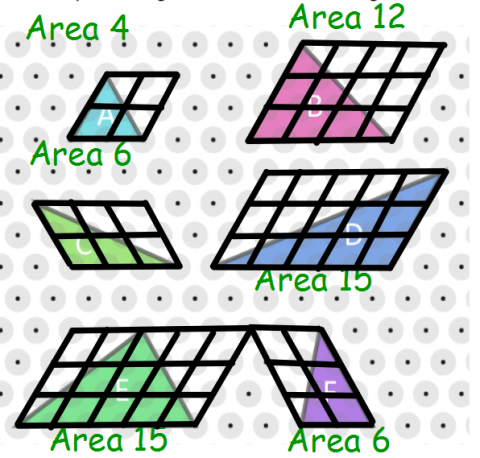
Each of the triangles below has at least two edges whose side lengths are whole numbers.
For example triangle $B$ has sides of length $3$ and $4$.

Work out the area, in terms of $T$, of each of the triangles.
Compare the areas to the whole number side lengths.
What do you notice?
Can you explain what you have noticed?
You might like to try Of All the Areas next.
Getting Started
You might find it useful to take a look at Isometric Areas.
Can you see how you could join another identical (congruent) triangle to each triangle to form parallelograms?
How does the area of each triangle relate to the area of the parallelogram?
Student Solutions
Matt from Swindon Academy in the UK, Ambrose, Swiss and Piyush from West Island School in Hong Kong and Pete and Neha from International School of Lausanne in Switzerland found a formula for finding the areas of the triangles. Piyush said:
Area of a triangle on isometric paper = Whole number side length $\times$ other whole number side length
Pete and Neha, Matt and Ambrose used parallelograms to explain why this works. This is Ambrose's work:
For every triangle with at least two whole number sides, you can always form a parallelogram by putting 2 triangles together.

Then, from the task, "Isometric Areas", we know that the area of a parallelogram in "$T$" is $base\times height\times2$.
For the area of a triangle, we can divide this by $2$.
So the formula is: $base\times height$.
Matt thought about using small parallelograms, or 'squares', as units:

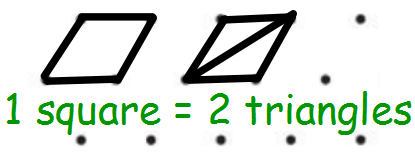
Swiss also thought about using little parallelograms as 1 unit of area:
To find the area of a normal triangle, the formula is b $\times$ h $\div$ 2 but since we're trying to find number of Triangles, you don't need to divide by 2 because 2$T$=1 unit of area.
Teachers' Resources
Why do this problem?
This problem, along with Isometric Area, invites students to look at area in a slightly different way from usual, using a triangle as the basic unit of area rather than a square, to reinforce the concept that area is about the space enclosed within a shape.
Along the way students have the opportunity to derive and justify a formula that they will not have met before.
Possible approach
This problem follows on from Isometric Areas
This dotty grid environment might be useful, and you can print off isometric paper for students. "On squared paper, it's easy to work out area by counting squares, but on isometric paper it's a bit different. If we want to compare areas of shapes drawn on isometric paper, we can use a small triangle as our unit of area, instead of a square!"
Show students this slide with the image from the problem. "These triangles all have at least two sides that have a whole number length. For each triangle, can you work out its area, measured in triangular units? How does the area relate to the length of the two sides that are whole numbers?"
Give students some time to work in pairs on the problem, sharing any useful strategies and conjectures that they come up with.
Finish off by bringing the class together to share their thoughts, and make the connection between the formula for the area of triangles in this problem, and the formula for the area of parallelograms in Isometric Areas.
Students may comment on the pairs of triangles with the same area, which are formed from splitting a parallelogram in half in two different ways (along each diagonal).
Key question
Can you see how you could join another identical (congruent) triangle to each triangle to form parallelograms?
How does the area of each triangle relate to the area of the parallelogram?
Possible support
Torn Shapes works with areas based on counting squares, so would be a useful task for students who are not confident with area.
Possible extension
Of All the Areas looks at the area of equilateral triangles with sides that are not whole numbers.
