Remarkable rectangles
Draw a triangle and construct a rectangle on its longest side. Use GeoGebra to explore how the area of the rectangle can change...
Age
14 to 16
Challenge level
Problem
If you are unfamiliar with GeoGebra, this article introduces the key ideas you will need for this problem.
Using GeoGebra, draw any triangle, and construct a rectangle on the longest side of the triangle with vertices on the other two sides:
Image
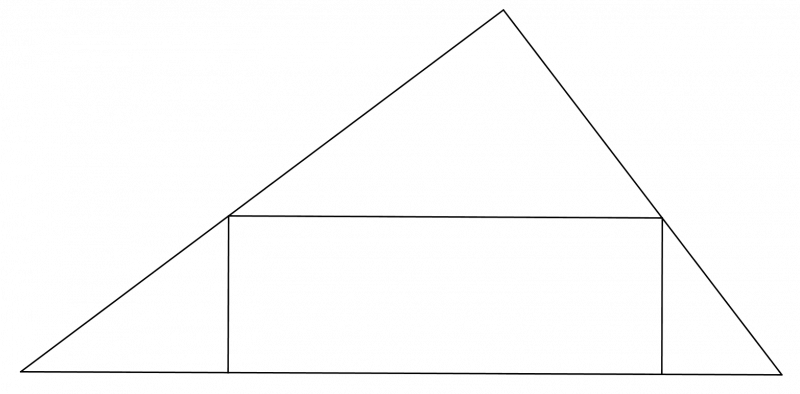
Use your GeoGebra diagram to explore how the area of the rectangle can change.
For a given triangle, how can you maximise the area of the rectangle?
How does this area compare to the area of the triangle?
Can you prove your findings?
Click below to see some diagrams that might help you to get started with your proof.
Image
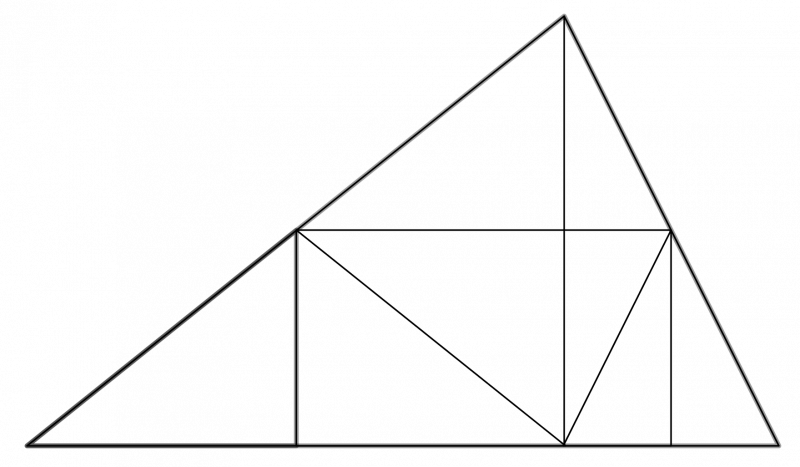
View interactivity
Getting Started
How can this interactivity help with your proof?
The three vertices of the triangle allow this to be altered. The vertex on the side allows the size of the rectangle to be changed.
The three vertices of the triangle allow this to be altered. The vertex on the side allows the size of the rectangle to be changed.