Squares in a Square
In the diagram, the small squares are all the same size. What fraction of the large square is shaded?
Age
11 to 14
Challenge level
Problem
Image
In the diagram, all the small squares are of the same size.
What fraction of the large square is shaded?
If you liked this problem, here is an NRICH task that challenges you to use similar mathematical ideas.
Student Solutions
There are a number of ways of solving this problem. One method is to count the unshaded squares in the diagram. There are $4$ complete squares, $8$ half squares and $4$ quarter squares, which is a total of $4 \times 1 + 8 \times \frac{1}{2} + 4 \times \frac{1}{4} = 4 + 4 + 1 = 9$.
Therefore there are nine shaded squares and nine unshaded squares, so half the area is shaded.
Image
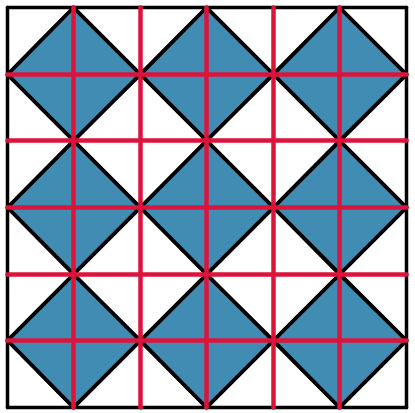
Alternatively, consider dividing the square up into the smaller red squares, shown in the diagram to the right. Each of the red squares is divided into two halves, one of which is shaded.
This means that half of the complete shape is shaded.