Tessellating triangles
Problem
We say that a shape tessellates if we can use lots of copies of it to cover a flat surface without leaving any gaps.
For example, equilateral triangles tessellate like this:
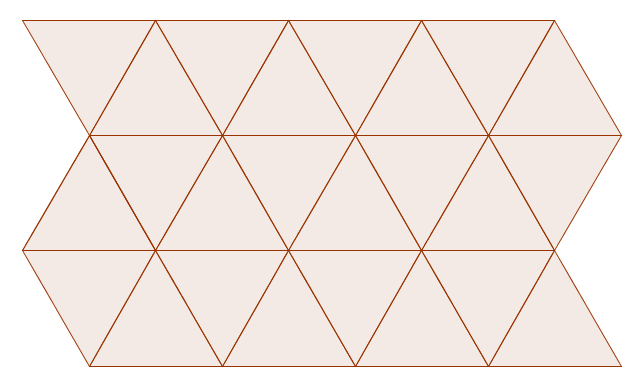
Let's think about other triangles which tessellate:
You can print off some square dotty paper, or some isometric dotty paper, and try drawing different triangles on it. You could also draw some triangles using this interactive.
Can you make your triangles tessellate?
Now try drawing some triangles on blank paper, and seeing if you can find ways to tessellate them.
Do all triangles tessellate?
If your answer is no, can you give an example of a triangle which doesn't tessellate and explain why it doesn't?
If your answer is yes, can you explain how you know that all triangles tessellate, and can you give an algorithm (a series of instructions) that you can use on any triangle to produce a tessellation?
You might find the interactivity below useful for this:
You can click and drag the corners of the triangle to change its shape, find the midpoint between two points, and rotate a shape around a point.
If you enjoyed this problem, why not take a look at Tessellating Quadrilaterals or Tessellating Hexagons?
For example, equilateral triangles tessellate like this:
Image

Let's think about other triangles which tessellate:
You can print off some square dotty paper, or some isometric dotty paper, and try drawing different triangles on it. You could also draw some triangles using this interactive.
Can you make your triangles tessellate?
Now try drawing some triangles on blank paper, and seeing if you can find ways to tessellate them.
Do all triangles tessellate?
If your answer is no, can you give an example of a triangle which doesn't tessellate and explain why it doesn't?
If your answer is yes, can you explain how you know that all triangles tessellate, and can you give an algorithm (a series of instructions) that you can use on any triangle to produce a tessellation?
You might find the interactivity below useful for this:
You can click and drag the corners of the triangle to change its shape, find the midpoint between two points, and rotate a shape around a point.
If you enjoyed this problem, why not take a look at Tessellating Quadrilaterals or Tessellating Hexagons?
