You may also like

Powerful Quadratics

This comes in two parts, with the first being less fiendish than the second. It’s great for practising both quadratics and laws of indices, and you can get a lot from making sure that you find all the solutions. For a real challenge (requiring a bit more knowledge), you could consider finding the complex solutions.

Discriminating

You're invited to decide whether statements about the number of solutions of a quadratic equation are always, sometimes or never true.

Factorisable Quadratics

This will encourage you to think about whether all quadratics can be factorised and to develop a better understanding of the effect that changing the coefficients has on the factorised form.

Quadrature of the Lunes

Age 16 to 18
Challenge Level

This resource is from Underground Mathematics.
 

 


A lune is the area left when part of a circle is cut off by another circle, as in the following problems.  It is called a lune because it looks a bit like the moon.

 

 

  1. In the following figure, two semicircles have been drawn, one on the side $AB$ of the triangle, and the other on the side $AC$ of the triangle (with centre $O$).  What is the area of the blue (shaded) lune which is bounded by the two semicircles?

    As a bonus, can you construct a square on the diagram with the same area as the blue lune, using only a straight edge (ruler) and compasses? This is called the quadrature (making into a square) of the lune.
     
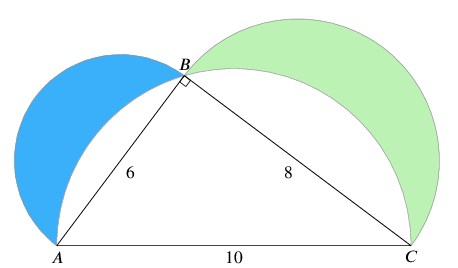
  2. In the following figure, three semicircles have been drawn, one on each of the sides of the right-angled $6$-$8$-$10$ triangle.  What is the total area of the two coloured (shaded) lunes in the drawing?

 

 

This is an Underground Mathematics resource.

Underground Mathematics is hosted by Cambridge Mathematics. The project was originally funded by a grant from the UK Department for Education to provide free web-based resources that support the teaching and learning of post-16 mathematics.

Visit the site at undergroundmathematics.org to find more resources, which also offer suggestions, solutions and teacher notes to help with their use in the classroom.

 

The NRICH Project aims to enrich the mathematical experiences of all learners. To support this aim, members of the NRICH team work in a wide range of capacities, including providing professional development for teachers wishing to embed rich mathematical tasks into everyday classroom practice.
Copyright © 1997 - 2023. University of Cambridge. All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.