The Third Dimension
Here are four cubes joined together. How many other arrangements of four cubes can you find? Can you draw them on dotty paper?
Problem
Here are four cubes joined together:
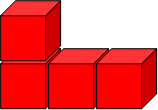
We can draw this arrangement of cubes on dotty paper (isometric paper) which gives us a way of drawing 3D objects more easily:
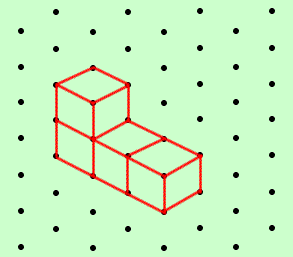
How many other arrangements of four cubes can you find?
Can you draw them on dotty paper? It's more difficult than it looks!
If you don't have any isometric paper, you can find some on our printable resources page, or you could use the interactivity below to draw your arrangements.
Getting Started
Use multilink cubes to make the arrangements. Keep each one so you can make sure they're all different.
When you have drawn your arrangements on dotty paper, try giving them to a friend. He or she can make the shapes as a check to see whether you've drawn them correctly.
Student Solutions
| Lots of you sent us excellent solutions for The Third Dimension. Chris and Michael from Moorfield Junior School, and Lily and Ruth from Brecknock Primary School in Camden managed to find eight arrangements altogether, including the one which we drew in the question. Lily explains how she systematically looked for them all: |
|
| Here is Ruth's drawing which shows these arrangements very clearly: |
Image
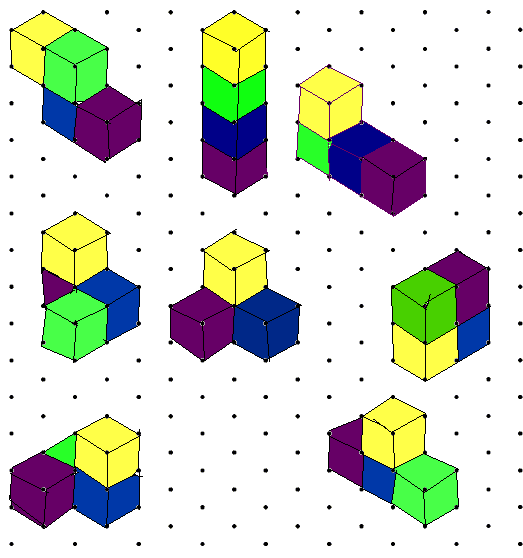
|
Ciara (from Bristol) explained her strategy:
First I built a tower with multilink where all four blocks were in a row. I called this 'The Tower'. Then I kept three in a row and moved one block into other possible positions. I gave them both names and this helped me with spotting if I'd done any repeats.
When I'd found all of these, I tried versions where there were no more than two blocks in a row. The names were really useful especially with the 'Staircases' as I realised there were two different ways of building the staircase.
In total I found 8 different possibilities for arranging four cubes.

Thank you for these good solutions. Well done !
Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible extension
Possible support
Some pupils might find it easier to try Building Blocks before starting this activity.
