Coloured edges
The whole set of tiles is used to make a square. This has a green and blue border. There are no green or blue tiles anywhere in the square except on this border. How many tiles are there in the set?
Problem
| There is a set of tiles which are all different and coloured just on the edges. Each edge on a tile is a different colour. For example: |
|
Image

|
| Altogether $10$ different colours are used for the edges, and there is an equal number of edges of each colour used throughout the set. |
| The whole set of tiles is used to make a square. This has a green and blue border. There are no green or blue tiles anywhere in the square except on this border. |
|
Image
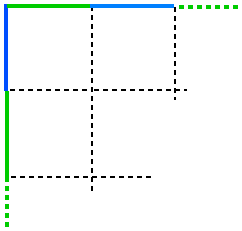
|
| How many tiles are there in the set? |
Getting Started
| What sort of number of tiles must you use to make a square? |
| What sort of number of tile edges must fill the perimeter of the square? |
Student Solutions
Laura Turner and Laura Malarkey from the Mount School have explained how they worked out the answer to this problem:
n is equal to the number of tiles along one side.
We can calculate the number of edges in two different ways:
Method 1 - In total there are $n ²$ tiles on
$4n ²$ edges.
Method 2 - There are a total of $2n$ green edges which implies
there are a total of $20n$ edges of all colours.
Therefore:
$20n = 4n ²$
$5n = n ²$ (divide by $4$)
$5 = n$ (divide by $n$)
So there are $25$ tiles in the set.
Teachers' Resources
Why do this problem?
This problem requires learners to work logically with numbers and shapes at the same time. The best ways of finding a solution include using a letter to represent the length of the side of the square.Key questions
What sort of number of tiles must you use to make a
square?
What sort of number of tile edges will make up the perimeter
of the square?
Have you thought of using a letter to represent the length of
the side of the square?
