Star Polygons
Draw some stars and measure the angles at their points. Can you find and prove a result about their sum?
Problem
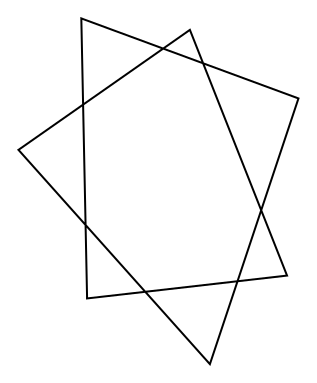
Here is a five-pointed star:

Draw a couple of five pointed stars of your own, making sure your lines are nice and straight!
Measure the interior angles at the five points and add them together.
What do you notice?
You may find this set of slides from Karen Hancock useful - they show how you can use the Desmos geometry construction tools to tackle this problem.
Here is a seven-pointed star:

Draw some seven-pointed stars of your own.
Measure the interior angles at the seven points and add them together.
What do you notice? Can you explain your findings?
You might find the animation below helpful:
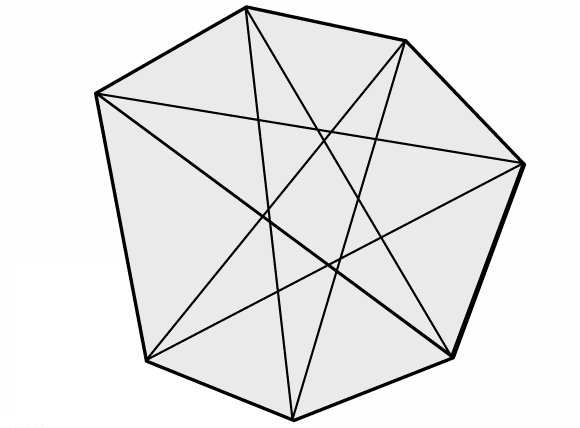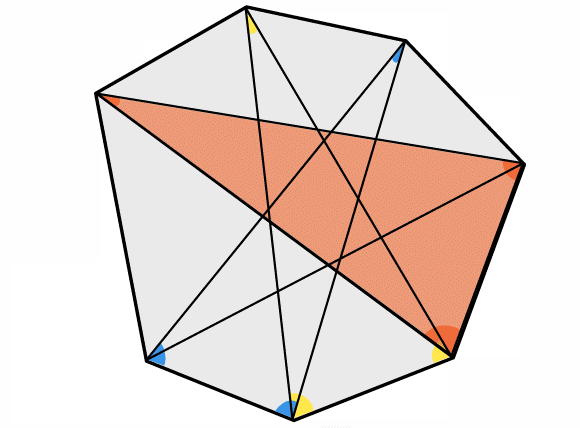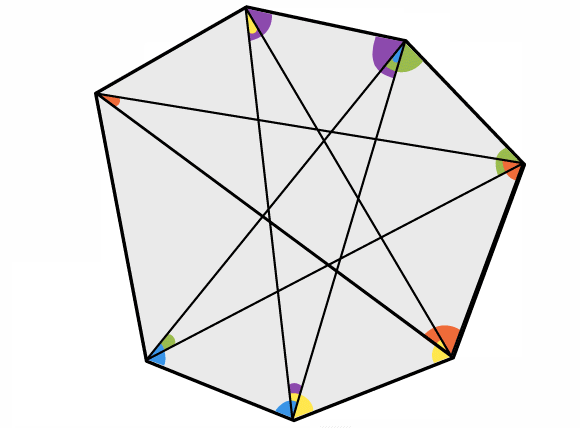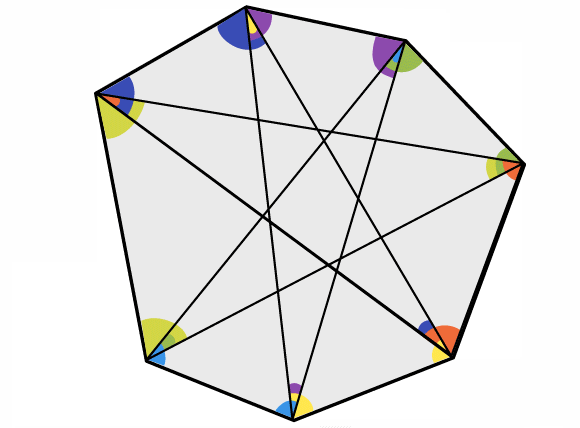
Click below to reveal a picture from the end of the animation:

Can you state and prove similar results for any other types of stars?
Getting Started
If you know the five interior angles of the pentagon, what other angles can you work out?
What do you know about the angle sum of a pentagon?
Could algebra help?
Student Solutions
Well done to Rose from Newstead Wood School in the United Kingdom and Melissa from Bangkok Patana School in Bangkok who sent us their solutions to this problem. They both used different methods prove this result.
Here is Rose's proof for the five-pointed star:
Notice there is a pentagon in the centre of the five point star. The exterior angles of this shape must add up to $360^\circ$. If the exterior angles are marked onto a diagram, each one is in a corner of an outer triangle, as shown below:
Effectively, there are two sets of exterior angles on the central pentagon, depending on the direction in which they are marked. Mark these in (shown in pink and blue on the diagram above) and each outer triangle will have an angle drawn in two base corners. There are are five triangles within a five-pointed star. The angles in a triangle add up to $180^\circ$. $180^\circ \times 5$ will give the total number of degrees in all the triangles of the star: $900^\circ$
Earlier, it was said exterior angles on the central pentagon had to equal $360^\circ$. Two sets of exterior angles have been marked on the shape. If both of these sets are subtracted from the total angles: $900^\circ - 360^\circ - 360^\circ = 180^\circ$ is left. This is the sum of the outer points of the star.
Melissa sent us the following proofs for the five- and seven-pointed stars:

Teachers' Resources
Why do this problem?
This problem offers a nice opportunity for students to practise measuring angles in a situation that leads them to make a discovery that they can then try to prove.
Possible approach
Show the image of the five-pointed star from the problem or draw one, and invite students to draw stars of their own. Ask them to measure the angles at the points as accurately as they can, and then add the five angles together. Collect some of their results on the board.
"It looks like the answers are all around $180^{\circ}$. I wonder if we can prove it?"
There are a number of options for proving the result. Students could create a diagram in GeoGebra and use it to gain insights about how the different angles change when they change the star.
Students could be encouraged to label the angles in their diagram and use angle rules to write down relationships between the angles. How do these relationships relate to the result they are trying to prove?
Some students may wish to consider the special case of a "regular" star whose points lie at five equally spaced positions on a circle.
Bring the class together to discuss proof methods and share ideas. Then perhaps go onto the seven-pointed star. The animation in the problem shows one way of proving the result for a seven-pointed star. The total of the angles in the 7 triangles is the same as the sum of the interior angles of the heptagon and twice the sum of the angles at the points of the star.
Alternatively, some students may wish to consider the angle turned through as they mentally "walk" around the lines of the star.
Key questions
If you know the five interior angles of the pentagon, what other angles can you work out?
What do you know about the angle sum of a pentagon?
Could algebra help?
Possible support
Polygon Pictures offers students practice in calculating angles in regular polygons.
Possible extension
Students could investigate stars with more points, or different types of stars made by joining points around a circle differently. For example, the two stars below have been created by plotting seven points around a circle, and in the first image joining every third point, and in the second image joining every second point.