Completing Quadrilaterals
We started drawing some quadrilaterals - can you complete them?
Problem
Completing Quadrilaterals printable sheet
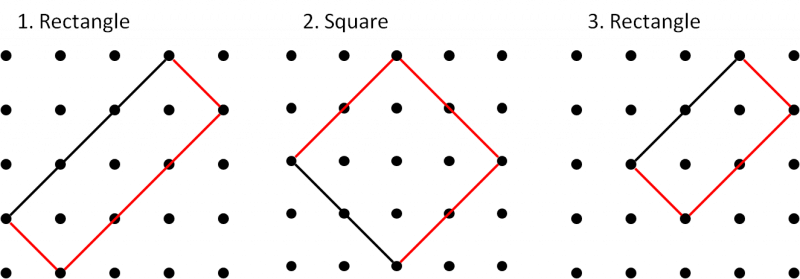
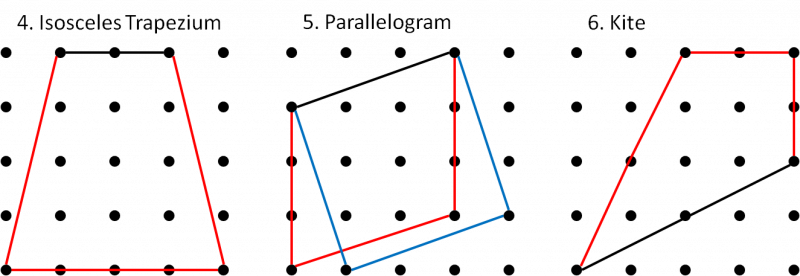
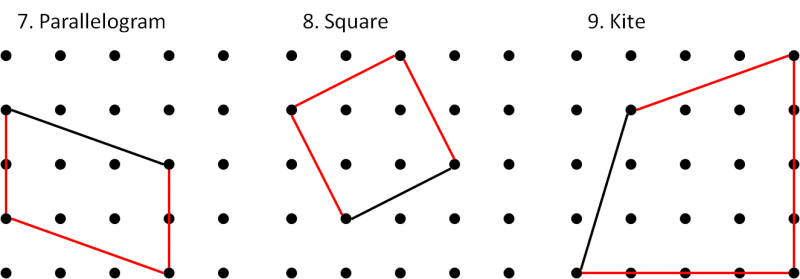
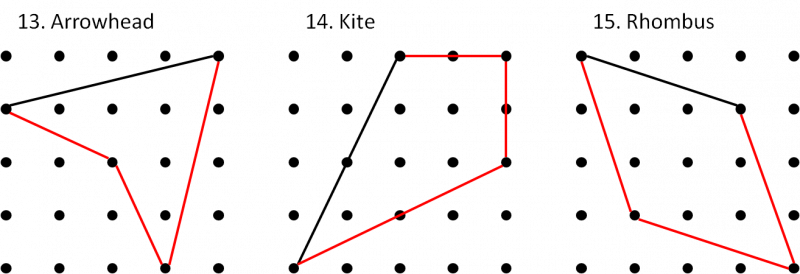
Each line is one side of the named quadrilateral. Can you draw the other three sides in the 4 by 4 dotty grids?
If there is more than one possibility, try to find the quadrilateral with the largest area (given in brackets).
An * indicates that there is a "special" quadrilateral with a larger area than the one given in the brackets. For example, the largest parallelogram might be a square or a rectangle. Take a look at the Getting Started page if you want to find out more about special cases.
| 1. Rectangle (6) | 2. Square (8) | 3. Rectangle (4) |
Image
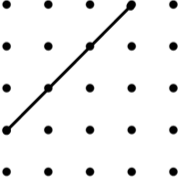
| Image
| Image
|
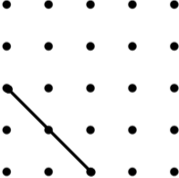
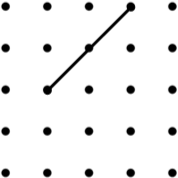
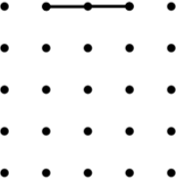
4. Isosceles Trapezium (12) | 5. Parallelogram (9*) | 6. Kite (8) |
Image
| Image
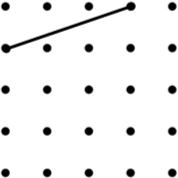
| Image
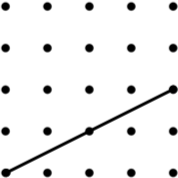
|
7. Parallelogram (6) | 8. Square (5) | 9. Kite (12) |
Image
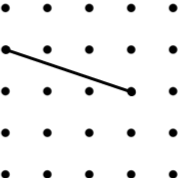
| Image
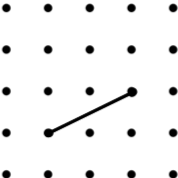
| Image
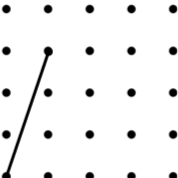
|
10. Rhombus (4*) | 11. Parallelogram (3*) | 12. Kite (6) |
Image
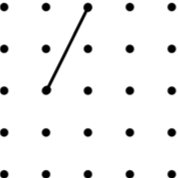
| Image
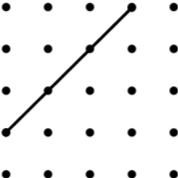
| Image
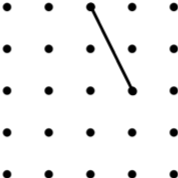
|
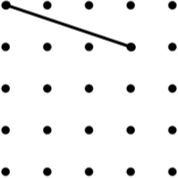
13. Arrowhead (6) (Concave Kite) | 14. Kite (8) | 15. Rhombus (8) |
Image
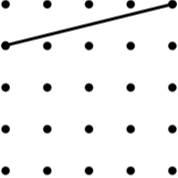
| Image
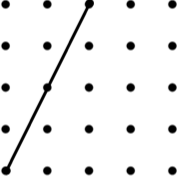
| Image
|
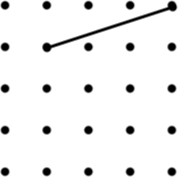
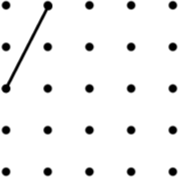
16. Rhombus (3) | 17. Arrowhead (4) (Concave Kite) | 18. Trapezium (9) |
Image
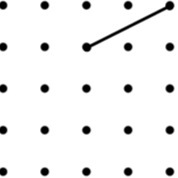
| Image
| Image
|
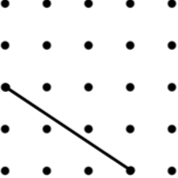
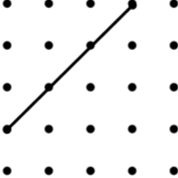
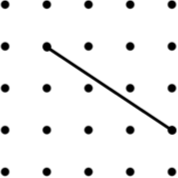
19. Parallelogram (8) | 20. Isosceles Trapezium (8) | 21. Kite (3) |
Image
| Image
| Image
|
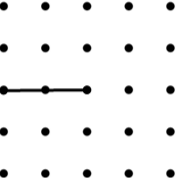
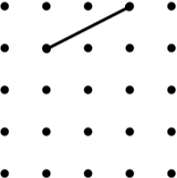
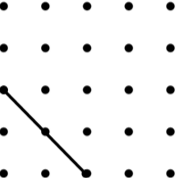
22. Arrowhead (4) (Concave Kite) | 23. Kite (9) | 24. Trapezium (9) |
Image
| Image
| Image
|
With thanks to Don Steward, whose ideas formed the basis of this problem.
Getting Started
Special Cases
How do you define a rectangle? There are lots of possible definitions, such as:
A quadrilateral with four right angles.
Does a square satisfy this definition?
Answer: yes!
This means that a square is a special type of rectangle: it meets all of the criteria for a rectangle but has other special properties. Take a look at these rectangles:

One of these is special, and is given the extra name of a square, but it is still a rectangle. It is a special case of a rectangle.
Notice that all squares are rectangles, but not all rectangles are squares. Think about the right-hand rectangle above.
Here are some other examples of special cases:

These are a collection of rhombuses, one of which is also a square.

These are a collection of kites, one of which is also a rhombus.

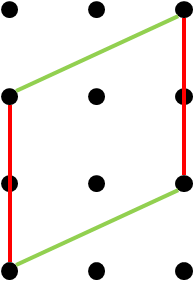
This is a collection of parallelograms, one of which is also a rectangle.
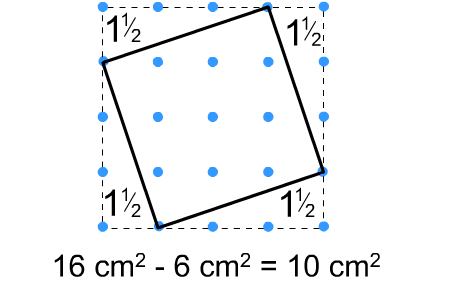
Two standard methods for working out the areas of tilted squares, which may help to work out the areas of the quadrilaterals:
Splitting the tilted square into right-angled triangles and squares and adding the areas of the different parts:
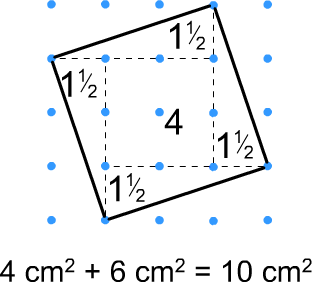
Boxing in the square, working out the area of the box and subtracting the areas of the unwanted right-angled triangles:
Student Solutions
Solutions to this problem were received from Emma, Rebekah and Charlotte, all of Wycombe High School, Julian, from the British School Manila in the Philippines, Ian, from Canberra Grammar School, Australia, and Zach. Thank you and well done to them!
The solution presented below is a combination of all of their solutions.
You will have made a decision about whether to allow special cases in your solutions, such as allowing a square when a rectangle is asked for. Take a look at the Getting Started page if you want to find out more about special cases.
In the solutions below, the red shapes exclude special cases. Where there is a special case that is larger, that shape is given in blue.




One common mistake was to make a shape where the sides were not quite of the same length. For example, consider the shape below:
Teachers' Resources
Why do this problem?
This problem is an engaging consolidation activity - it challenges students to apply their knowledge of the properties of quadrilaterals, and to work systematically to identify possible quadrilaterals, while trying to maximise their areas on a small dotty grid.
Possible approach
The following printable worksheet may be useful: Completing Quadrilaterals.
You may like to play a couple of rounds of Guess my Quad with your class at the start of the lesson to clarify the properties of different quadrilaterals.
This may offer an opportunity to discuss nested categories of shapes: a square is a "special" rhombus, so if a rhombus is chosen, will students permit "square" in response? See Getting Started.
Before handing out the worksheet, you may also wish to discuss with students how they can work out areas of shapes on a dotted grid.
The images below might provide a useful prompt - they demonstrate two alternative ways of working out the area of tilted squares:


Lexy from QK Academy shared these ppt slides that she used with her class when they were working on this problem.
Key questions
What properties does a square / rectangle / parallelogram / kite / rhombus / trapezium / arrowhead have?
Is a square a special rectangle?
Is a rectangle a special parallelogram?
Is a rhombus a special kite?
Possible extension
These three problems provide suitable follow-up challenges:
Isosceles Triangles
Triangles in a Square
Square it
Possible support
Starting by playing Guess my Quad, in which students use properties of quadrilaterals to guess their opponent's shape using as few questions as possible, would offer an opportunity to clarify the properties of different quadrilaterals.
Students could start with the shapes they are more confident with (perhaps squares, rectangles, parallelograms and kites) before tackling the rhombuses, trapezia and arrowheads.
