Perimeter Challenge
Can you deduce the perimeters of the shapes from the information given?
Problem
Perimeter Challenge printable sheet
In each of the following problems, work out the perimeter of one small rectangle:

(a)
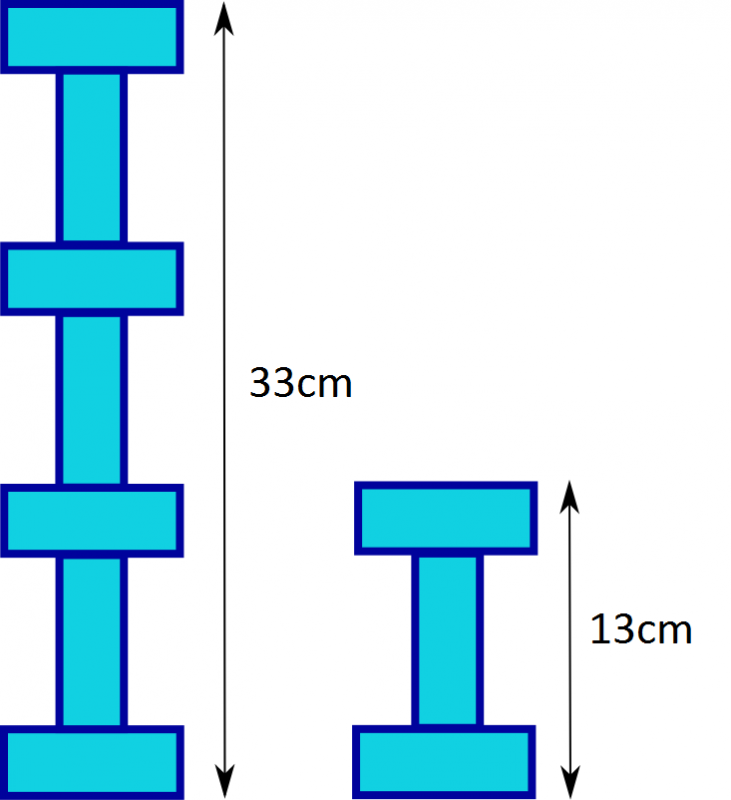
(b)

(c)

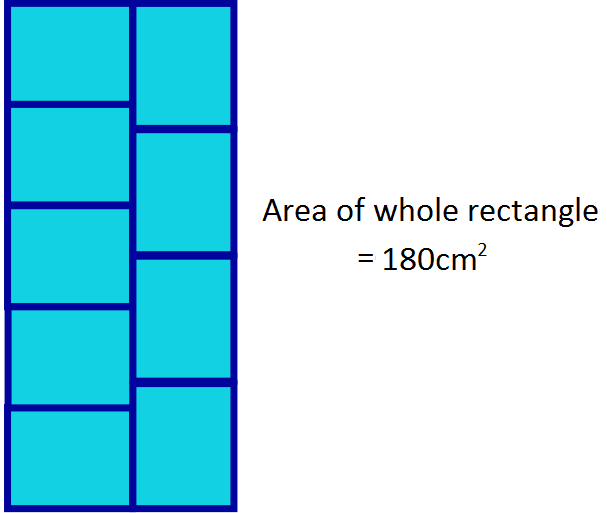
(d)
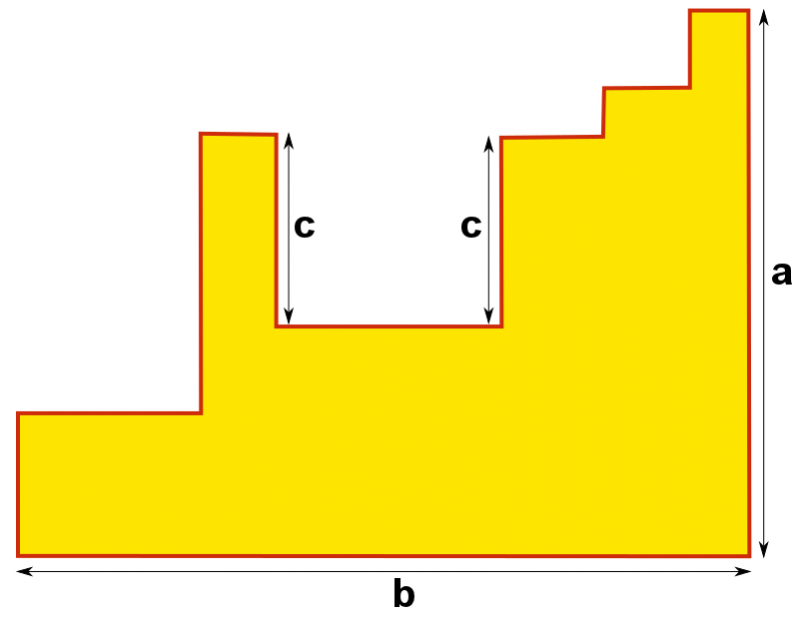
Can you find the perimeter of this shape?
You may wish to try Perimeter Possibilities next.
With thanks to Don Steward, whose ideas formed the basis of this problem.
Student Solutions
Lots of people submitted solutions to this problem - thank you everyone! There were too many good solutions to name everybody, but we've used a selection of them below:
David from Sacred Heart Catholic College used algebra to solve part (a):
There are two values: $W$ (the width of the small rectangle) and $L$ (length of the small rectangle).
The height of the $1^{st}$ tower is made of $4W$ and $3L$, which equal $33$ ($4W + 3L = 33$)
The height of the $2^{nd}$ tower is made of $2W$ and only $1L$. They equal $13$ ($2W + L = 13$)
So If we double the second tower then we will have $4W$ but only $2L$. It will
equal $26$ ($4W + 2L = 26$).
Therefore if we take away double the second tower away from the first
tower, we will have one length and it will measure $7cm$. ($L =(4W + 3L) - (4W + 2L) = 33-26 =7$).
Now that we know what one length is, we can substitute $L=7$ into our equation for the height of tower $2$ ($2W + L = 13$).
If we take away the $7$ we will have $2W = 6$. Then you divide both sides of this equation by $2$ to find $W=3$.
To work out the perimeter, you will need to add $2W$ and $2L$.
This is $2\times 3 + 2\times 7$, equal to $\textbf{20cm}$.
Yueyang from CJS used a similar method to solve part (b):
You can see that there are five rectangles. Since their
combined area is $60cm^2$, this means that the area of one of the five
rectangles is $12cm^2$.
Then, we can see that the length of one rectangle
is the same as three widths. If $x$ is the length of the triangle and $y$ is the width, we can now form the equations:
$xy = 12$
$x = 3y$
Thus, we can substitute $x$ with $3y$, turning the first equation in to $3y^2 = 12$. Divide each side by $3$ to make $y^2=4$. The square root of $4$ is $2$, so the width of the rectangle is $2$. In that case, as $x$ is $3$ times $y$, the length of the rectangle is $6$. Therefore, the perimeter will be $2+6+2+6$ which is equal to $\textbf{16cm}$.
Here's how Care, Nika and Brian from British International School Phuket solved part (c):
If we call the length of the rectangle $b$ and the width $a$ then we can see $4a = b$.
Then the width of the big rectangle is $4a+2a=6a$ and the area is $6a \times 4a = 24a^2 = 600$.
Then $a^2 = 25$
So $a = 5mm$
$b = 4a= 20mm$
and perimeter of rectangle = $\textbf{50mm}$
Tyler, Katie, Jennifer, Peter and Zach from Lab School thought about factors to solve part (d):
Step $1$: We read the area of shape (d), which was $180cm^2$.
Step $2$: We came up with the equation $x= \frac{4}{5}$ of $y$. In this equation $x$
represents the shorter side of the rectangle and $y$ represents the longer sides. This is
true because the height of the large rectangle equals either $5$ shorter sides or $4$ longer
sides.
Step $3$: We found out that the area of each small rectangle is $20cm^2$,
because $9$ small rectangles equal $1$ large rectangle, and $180 \div 9=20$.
Step $4$: We found all the factors of $20$ and paired them up: $1$ and $20$, $2$ and $10$, $4$ and $5$.
Step $5$: We found out that only one pair of the factors follows rule of one number being $\frac{4}{5}$ of the other. These factors are $5$ and $4$.
Step $6$: So the perimeter of the small rectangle is $4+5+4+5=18cm^2$.
Paula and Kiera from Hinchley Wood drew a diagram to show how they found the perimeter of the final shape:
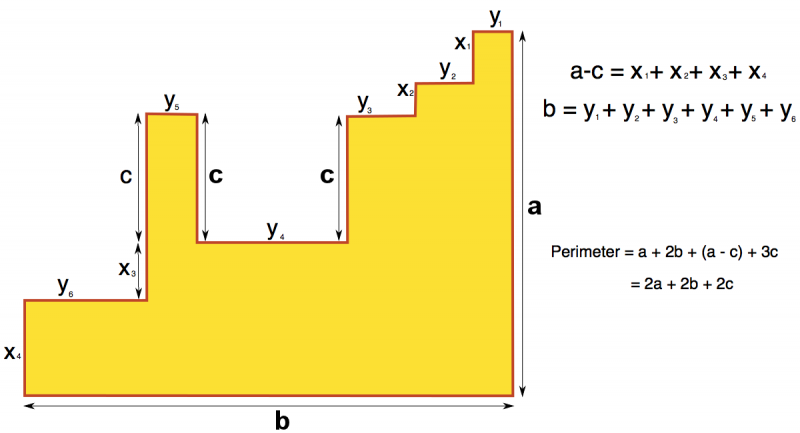
Thank you again to everybody who submitted a solution!
Teachers' Resources
This printable worksheet may be useful: Perimeter Challenge.
