Transformation Tease
Problem
Here is a set of axes with one shape drawn in the first quadrant:
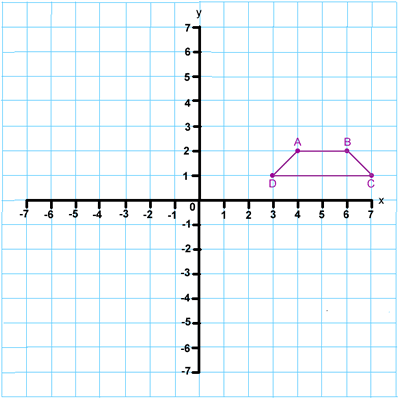
What is this shape called? What are the coordinates of the points A, B, C and D which form the corners of the shape?
Translate (or move) the shape 3 squares to the left and 4 squares up. What are its new coordinates?
Compare these with the original coordinates. What do you notice about the numbers?
Start with the shape above again. This time reflect it in the x axis. What are the coordinates of the corners now?
What do you see when you compare these coordinates with the original ones?
Predict what the new coordinates would be after a reflection in the y axis.
Plot these three points on the graph:
(-7, 7)
(0, 0)
(7, -7)
Join the points to make a straight line.
This line is called y = -x because at any point on the line the x coordinate is the same as its y coordinate, but negative.
Reflect the starting shape in the line y = -x and give the new coordinates for A, B, C and D.
Look carefully at these new coordinates and then predict what would happen to these points if they were reflected in the line y = -x:
(2, 4)
(6, -4)
(-5, -5)
Now take the original shape again and rotate it 90 o anticlockwise about the origin. What do you notice about the new coordinates?
How else could you describe this transformation?
Getting Started
After each transformation (translation, reflection or rotation), look at each point and ask yourself:
- What has happened to the x coordinate?
- What has happened to the y coordinate?
Student Solutions
Amy, David, Euan, Lewis and Robert at St. Nicolas School, Newbury tried solving this problem. They have explained their solution very clearly although it is quite long!
