Beach Huts
Can you figure out how sequences of beach huts are generated?
Problem
Beach Huts printable worksheet
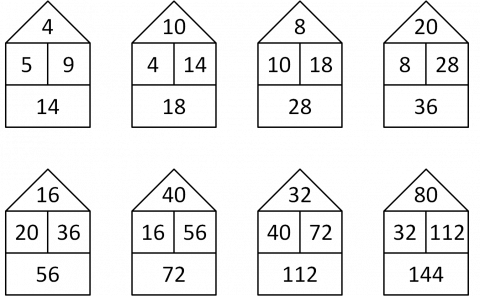
A "beach hut" is generated from its two middle numbers.
Can you figure out the rule for working out the roof and floor numbers?

These beach huts form a sequence. Can you see how the second hut follows on from the first? And how the third hut follows on from the second?
Can you find the next huts in the sequence?
Do you notice any interesting patterns?
Try making some sequences of huts starting with your own numbers in the middle two boxes.
Do these sequences follow similar patterns?
If you have a beach hut from the middle of a sequence, is there a way to work out the beach huts that came before it?
Here's one to try:

Here are some questions you might like to consider:
If you know any pair of numbers from a beach hut, can you work out the other two numbers?
Can you find a sequence of beach huts where two adjacent huts have the same roof number?
If you know the numbers in a hut, how can you work out the numbers of the fourth hut to the right of it? Or the 10th? Or the 100th...?
If you know the numbers in a hut, how can you work out the numbers of the sixth hut to the left of it? Or the 12th? Or the 100th...?
If you know the numbers in a hut, how can you work out the numbers of the seventh hut to the right of it? Or the fifth hut to the left of it? Or the 99th in either direction...?
With thanks to Don Steward, whose ideas formed the basis of this problem.
Student Solutions
Thank you and well done to everyone who submitted solutions to this problem. Far too many of you sent in solutions to mention all of you, but there were lots and lots of good ideas.
Gavin, from Woodhaven School in Canada, described how the numbers in each hut are related:
The answer for the hut is the roof is the difference between the 2 blocks in the middle of the house. Then the two blocks in the middle added together makes the bottom number.
Ruby, Hannah and Emma, from Berkeley Primary School, used algebra to relate these numbers:

They found the following relationships:
B-A&=&X\\
B+A&=&Y
\end{eqnarray}$
Jared, from Associated Hebrew Schools in Canada, was able to relate each hut to the subsequent hut:
$X$ is always the same as $A$ in the next hut. $Y$ is always the same as $B$ in the next hut.
Ruby, Hannah and Emma described this pictorially:

Many of you were able to find the next few huts using these rules:
Tom, Morgan and Libby, from Berkeley Primary School, had a different way of explaining the patterns in the beach huts.

The 5 swaps places with the 4, and the 5 then doubles.
As for the 9 and the 14, they swap too, and the nine doubles. Now you have the numbers in place for the next hut. Then you do the same for the next hut, just with different numbers.
Mackenzie, from Queen Elizabeth's Hospital School, noticed a pattern when you move two stacks to the right:
The odd term huts follow a pattern and the even term huts also follow a pattern. For example, if you knew the fifth term hut then you could easily find the seventh hut by doubling all of the numbers in the fifth. This also worked for the even term huts, e.g. tenth hut is double the eighth. Therefore in order to find the 100th term (even number) we needed to double the numbers in the second hut 50 times.
Patrick, from Hitchin Boy's School, was then able to express the value of the numbers in the 100th hut to the right algebraically:
You have to move to the right 100 huts. Since moving two to the right doubles the number, you need to multiply the numbers in the second hut by two 50 times, or by $2^{50}$.
Kelly and Beth, from Loughborough High School, used algebra to check that this doubling always takes place:

The third beach hut is then always twice the third beach hut, so moving two huts to the right always doubles the number.
Imesh, from Roding Primary School, was able to describe how to go backwards from one hut to the previous one:
To find the beach hut before the one given, the left number in the middle floor is the same as the roof in the hut before it and the bottom floor in the hut before is equal to the number of the right number in the middle floor in the given hut. As you found the bottom and top numbers, to find the left middle floor number in the hut before you do the bottom number subtract the top number divided by two. Finally, to get the right number in the middle floor, you should subtract the left middle-floor number from the bottom number.
7Y, from Queen Elizabeth's Hospital School, were able to explain how to go back many huts to the left.
After this we considered going in the opposite direction (to the left) and quickly deduced that we just needed to reverse
the operation of (doubling) and divide each number by two instead in order to move left by two huts.
Zach was able to use this to find many of the different terms. You can see his solution here, and the second part here .
Teachers' Resources
Why do this problem?
This problem invites students to look at a few examples, notice and explain patterns, and then generalise. Many questions about sequences just look at a single variable. As each beach hut contains several linked numbers, there are several different sequences to spot and explain.
Possible approach
Display the first image of beach huts.

"Here is a sequence of beach huts. Take a moment to look at them and see what you notice."
"Now turn to your partner and discuss what you noticed. Did you see the same things?"
"With your partner, see if you can agree what the next beach hut in the sequence might look like."
Once students have had a chance to draw the next beach hut, take some time to discuss everything they noticed, and agree as a class how the numbers in a hut are related and how each hut is related to the previous one.
Here are some questions that you may wish to invite students to explore:
- If you know any pair of numbers from a beach hut, can you work out the other two numbers?
- Can you find a sequence of beach huts where two adjacent huts have the same roof number?
- If you know the numbers in a hut, how can you work out the numbers of the fourth hut to the right of it? Or the 10th? Or the 100th...?
- If you know the numbers in a hut, how can you work out the numbers of the sixth hut to the left of it? Or the 12th? Or the 100th...?
- If you know the numbers in a hut, how can you work out the numbers of the seventh hut to the right of it? Or the fifth hut to the left of it? Or the 99th in either direction...?
To work on these questions, students could generate sequences of beach huts of their own and look for rules linking the numbers between huts. You may wish to introduce an algebraic representation where the middle two numbers in the hut are $a$ and $b$, and invite students to work out other terms in the sequences algebraically.
At the end of the session, bring the students together and set them a challenge: "Here is a beach hut. Without drawing all the huts in between, quickly draw for me the 5th and 8th hut to the right." If you have mini whiteboards the students could draw their huts and then hold them up to see if everyone agrees. Finally, invite students to compare how they worked out the numbers.
Possible support
Encourage students to draw the next few beach huts in the original sequence and look for as many different patterns as they can, before trying to explain those patterns.
Challenge them to go both to the right and to the left.
