What's x got to do with it?
Algebra in the national curriculum
Anne Watson (Emeritus Professor of Mathematics Education, University of Oxford)
The purpose of this article is to make explicit some of the aspects of algebra, particularly for young children, that need attention if more students are going to adopt an algebraic approach to mathematics as standard. By following through the threads of algebraic thinking, discussed in this article, from early primary through to secondary formal algebra we can ensure that children's mathematical
experiences follow a continuous progression. The paper also explores the use of Cuisenaire rods and graphplotters to support children’s understanding.
Research references can be found in an extensive document published by the Nuffield Foundation (http://www.nuffieldfoundation.org/sites/default/files/P6.pdf).
Historical background: a personal perspective
No sooner was the new mathematics NC off the starting blocks than I began to hear stories about primary teachers being advised that in year 6 they need to be teaching '$y=mx+c$'. That may be what Gove imagined, and it was certainly in early drafts of the NC, but year 6 is either too early or too late for this. It depends on whether this means that students should be working in a variety
of informal ways with linearity, or that students should be grappling with formal notation and formal treatment of straight line graphs and linear functions. For the former it is too late and for the latter too early.
The specialist panel (on which I sat) was given limited time and resources to develop a workable curriculum that was true to mathematics, and we had to translate everything into language that could be understood by civil servants and politicians. Throughout our work we tried to establish some fundamental ideas about algebra that avoided the need to fly in '$x$' as some kind of symbolic alien in
year 6 and instead builds on students' understanding of relations among quantities. In KS1 and 2 we were able to give some guidance about this but in KS3 we were prevented from providing guidance to explain the thinking behind the list of topics. At first glance it certainly looks as if what is required at KS3 is old-fashioned manipulation practice followed by some graphing. For some time we had
included a 'pre-algebra' strand in primary to try and emphasise that algebra is a way of expressing generalities and relationships, but those ideas were absorbed into other headings and became rather hidden.
The Advisory Committee on Mathematics Education (ACME), in its responses to consultations about the NC, advised:
• Expectations of algebraic thinking could be based on reasoning about relations between quantities, such as patterns, structure, equivalence, commutativity, distributivity, and associativity
• Early introduction of formal algebra can lead to poor understanding without a good foundation
• Algebra connects what is known about number relations in arithmetic to general expression of those relations, including unknown quantities and variables.
These statements were an informed reaction to statements from Ministers that algebra had to be taught to younger students in order to match the curricula of high performing jurisdictions. Ministerial statements ignored the fact that the basics of algebraic reasoning had always been in our earlier versions of the national curriculum and many of these pre-algebraic ideas appeared earlier in
England and Wales than in those countries ministers sought to emulate. The difference of opinion hinged around what can be described as algebra.
As the ACME comments above make clear, school algebra is founded on expressing structure, equivalence, and laws of combination of operations. These concepts emerge in early learning about number and arithmetic. Students' arithmetical competence and inventiveness depend on them, and they can develop further through mental methods and a range of spatial models for number.
Rather than being explicit about this as we would have wished, we ensured that there are indications throughout the primary curriculum in the guidance that can be read as directions to develop an algebraic, structural, understanding of number and arithmetic.
Algebraic indicators in the NC
Here are some examples mentioned in the NC:
• patterns in the number system; repeating patterns with objects and with shapes
• several forms of relations between quantities (e.g. 9 + 7 = 16; 16 – 7 = 9; 7 = 16 - 9)
• proper use of equals sign
• addition/subtraction and multiplication/division as pairs of related operations
• the effect of adding or subtracting zero
• commutativity and associativity of addition (e.g. 1 + 3 + 5 = 3 + 1 + 5 etc.)
Most of these ideas are met in early number, with concrete materials and structured apparatus such as Cuisenaire rods and numberlines.
Further examples:
• inverse relations (e.g. 4 × 5 = 20 and 20 ÷ 5 = 4)
• associative law (2 × 3) × 4 = 2 × (3 × 4)
• distributive law 39 × 7 = 30 × 7 + 9 × 7
These ideas can emerge through use of structured materials to learn the meaning of multiplication as arrays, and might be consolidated through problem solving, deriving mental methods, interpreting word problems, and - later - area considerations. Most of the guidance given for mental methods in the NC is algebraic as it is dependent on these laws and relations, but it may be
worthwhile for teachers to distinguish between those laws that are useful for all numbers, such as those above, and those that are useful in number-specific contexts, such as $n$ x 9 = $n$ x 10 - $n$ and so on.
The need for brackets
Also arising from number work is the need for brackets, for example to distinguish between, 2 + 1 x 3 = 5 and (2 + 1) x 3 = 9. Brackets can also be used to justify the former number-specific methods, so that $n$ x 9 can be written as $n$ x (10 - 1). (Here I am avoiding the standard notation of 9$n$ = (10 - 1)$n$ because adoption of conventional use of symbols is not the same as
understanding the underlying numerical relationships.)
Learning early algebra
So learning early algebra has two parts:
• the relations that need to be expressed
• the conventional ways to express them.
Much algebra teaching has focused on the second while ignoring the first, so that 'algebra' as a school subject appears to be a set of rules for moving letters around. As with any symbolic system (e.g. writing, or music, or dance moves) learning the system has to be connected with the meanings being communicated.
Missing number problems
The most obvious pre-algebraic aspect for people who think of algebra as 'solving equations' is the presence throughout the primary mathematics NC of missing number problems. However, it is important to note that there is extensive research about connections between:
• missing number problems that can be solved by filling in the gaps of known number facts, such as ∎ + 7 = 13 means that ∎ must be 6
• algebraic reasoning which involves transforming expressions and equations according to the laws of arithmetic, such as 158 = ∎ + 37
Moving from missing number problems by using '$x$' instead of an empty box can be seen as trivial but such a translation does not guarantee algebraic understanding. Rather it uses '$x$' as it might be used on a treasure map 'x marks the spot' or as a code. In easy examples involving integers students will use their knowledge of numberbonds to find the missing number, rather than
algebraic processes which enable them to work with all real numbers (and beyond).
Where's all this leading?
Before I talk further about primary algebraic experiences it is worth looking at where school algebra is expected to get to, as this gives some clues about where to focus attention on the way. A useful analogy is for everyone on a train journey to know that at the end of the journey people will have to describe the trees they saw on the way. Passengers, guard, announcer, catering staff, window cleaners and ticket information could all be helping with this and the train could slow down while it is passing a particularly tree-lined part of the route - but the main aim of the journey is to get from A to B. I am suggesting that algebraic and pre-algebraic ideas can be embedded, like tree-awareness, throughout the curriculum, and given special attention as they arise, but may not be the main aim of the lessons in which they appear.
GCSE content for algebra can be encapsulated into a few main headings:
• algebraic notation and manipulation
• solving equations in one variable and simultaneous equations in two variables
• sequences
• application of algebra, functions and graphs to real world problems
• properties and transformations of some simple functions.
The roots of these can be found throughout primary mathematics. Working backwards through the curriculum, I can identify eight key strands of algebraic learning and activity that apply, in a limited way, in primary mathematics too:
• Generalising relations between quantities
• Equivalence: different expressions meaning the same thing
• Solving simple equations (finding particular values of variables for particular states)
• Expressing real and mathematical situations algebraically (recognising additive, multiplicative and exponential relations)
• Relating features of graphs to situations (e.g. steepness and direction and turning points)
• Finding new relations from old
• Standard notation
• Understanding functions in general and some specified functions and their properties and behaviour
At least the first seven, and possibly the eighth if graphplotters are used regularly, can be introduced, referred to, and used in a planned and limited way throughout primary school, with a light touch, as the train team might indicate trees on the journey.
I am going to treat these as a 'boxed set' in abbreviated form for the rest of this paper.
equivalence
finding values
expressing situations
graphs to situations
new from old
standard notation
functions
And where does it start?
The explicit mention of algebra in the primary NC happens in the Year 6 programme of study:
• express missing number problems algebraically
• use simple formulae expressed in words
• generate and describe linear number sequences
• find pairs of numbers that satisfy number sentences involving two unknowns.
• enumerate possibilities of combinations of two variables
The accompanying non-statutory guidance makes it clear that it is expected that these should arise from situations that students already understand. Thus using letters is the mathematical way to communicate things that are known.
Introducing symbols and letters
Pupils should be introduced to the use of symbols and letters to represent variables and unknowns in mathematical situations that they already understand, such as:
• missing numbers, lengths, coordinates and angles
• formulae in mathematics and science
• arithmetical rules (e.g. $a + b = b + a$)
• generalisations of number patterns
• number puzzles (e.g. what two numbers can add up to).
CPD opportunity: whole-school progression 
For example, the mysterious statement about 'enumeration' refers back to guidance in year 1 about enumerating objects as an aspect of counting. This means arriving at a total not by counting every individual item but by grouping and combining or otherwise using number properties efficiently. For example, 12 as a quantity can arise from: 4 lots of 3, or 3 lots of 4; two groups of 6; 6
pairs; 2 lots of 5 plus two extra.
From this kind of work a need for notation can arise so we can say , in general, that if $c = ab$ then it also equals $ba$, and if it is even it can always be written as 2 x something. Furthermore, we could signify the 'something' using a letter and could then write $n$ as 2 x ($n$-1) + 2. All this and more can arise from manipulating blocks, or cuisenaire rods, or shading squares, or
mental arithmetic, or even by doing some traditional country dance patterns. The use of letters as the mathematical way to write things that are generally true arises from what is known and understood.
From the 'boxed set' this involves:
equivalence
expressing situations
new from old
standard notation
Working with number patterns
Another feature of primary mathematics that leads into algebra is work on number patterns. However there are several ways in which patterns and sequences pop up in primary work and it is important to distinguish between them. I have roughly classified them as:
• repeating
• continuing
• spatial
These distinctions, however, depend to some extent on what students are asked to do with them.
Repeating patterns:![]()
a, b, b, a, b, b, ...
doll, teddy, teddy, doll, teddy, teddy ....
Expressing this pattern in letters does not in itself make this an algebraic situation, but a question like 'What colour is the 17th square?' or a statement like 'every $(3n-2)$th square is red' is algebraic because it is relating position number to one of two values: red/blue; a/b; doll/teddy.
Continuing patterns:
1,4,7,10 ...
Expressing this pattern as 'add 3 each time' is an approach that generates the sequence, and relates to the later idea of gradient of a linear graph. Continuing patterns can be generated from multiplication tables, and from counting up and down in various step sizes, and graphs that represent these. The action of counting up and down can give a bridge between describing a linear sequence in
terms of multiplication, and describing it using the term-to-term generating rule.
We can also say that the $n$th term in this sequence has the value $3n-2$ (one more than the relevant multiple). It is worth comparing this to the ($3n-2$) in the example of repeating patterns as these have different meanings - they refer to different aspects of the sequence.
Spatial patterns:
Although it is possible to describe this pattern algebraically in two dimensions, it is far more likely that primary school students will want to describe it generatively (i.e. how you make it) or spatially (i.e. in terms of shape and relative position). It matters how this is valued in lessons - whether the teacher accepts spatial and ad hoc descriptions of sequences or whether s/he drives the
algebraic message of expressing relations.
From the 'boxed set' I have indicated:
expressing situations
graphs to situations
new from old
standard notation
functions
Learning to express and ‘read’ operations
Another aspect of primary mathematics which feeds algebra is in the ways we express and 'read' operations. If '=' is taken to be an instruction to calculate (‘makes’) then no bridge to algebra is being established and later on students will have to change their 'reading' of it. Cuisenaire rods can help move away from that reading towards an idea of equivalence.
Working with Cuisenaire rods
In the diagram below the additive relation between three quantities is represented in eight different ways. Each way denotes different physical actions. For example you can put down a red rod, then a yellow, and then find a rod that is the same length to equal it. Or you can put down a blue rod, then place a yellow next to it, and discuss how to 'fill the gap'. Different actions
relate to different meanings for subtraction, such as 'take away from' or 'find the difference between'.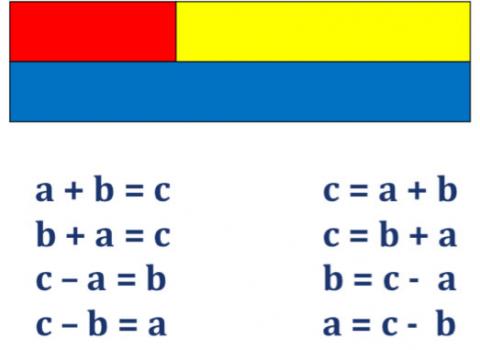
A student who has been consistently worked with these alternative expressions for the relationship will be well-prepared for expressing and manipulating with algebra later on. Similarly the multiplicative relationship below offers several different actions and perspectives which relate not only to algebraic manipulation (re-arranging formulae) but also to understanding ratio.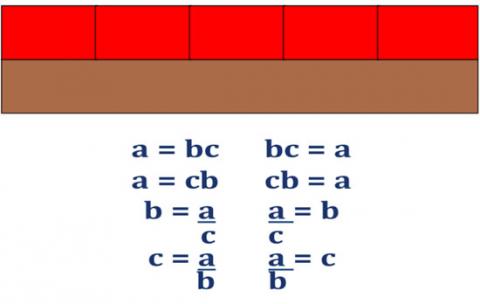
In these suggestions, which can be discussed using rods, measuring tape, and other linear models of number, the boxed set items in use are:
equivalence
finding values
expressing situations
standard notation
The additive relation can be extended easily. For example, giving students a line 18 cm. long you can ask:
Here is a line of a fixed length which is called L
Can you make lines of rods that are equal in length to L? Record your lines.
Can you make a line of length L using rods of only one colour? Record your lines.
Can you make a line of length L using rods of only two colours? Record your lines.
Methods of recording can generate a need for 'collecting like terms' so that a string written as 'green + green + green' can be written as '3green' to indicate a suitable notation.
Using mental arithmetic to develop children’s algebraic thinking
Mental arithmetic is a fertile ground for noticing and expressing algebraic relationships. With additive relations and multiplicative relations we have just seen commutativity appear, although with the red and brown rods we would need to construct a length equal to the brown rod using yellow rods to fully work it through. Two other laws of arithmetic that can be understood, used and
expressed are associativity and distributivity.
Associativity is often implicitly assumed. It means that if you have a string of numbers to add, or multiply, it doesn't matter which pair of numbers you start with to calculate the string. It does matter with mixed operations however and that is one of the reasons for using brackets to indicate which operation is to be done first, and also a reason for explicit instruction about
calculator use.
Distributivity arises throughout primary arithmetic: the main example is that if you add two numbers together and multiply by a scalar (another number) you get the same answer as if you had multiplied both of them by the scalar before you added. This idea is at the basis of much arithmetic and much algebra. It gives an entry into much traditional algebraic manipulation such
as $a(b+c) = ab + ac$ (multiplying out brackets and reversing the process by factorising). It provides insights into area, and vice versa. Its main role in mental methods is to chunk tricky numbers into helpful pieces, e.g. 39 x 7 = 30 x 7 + 9 x 7.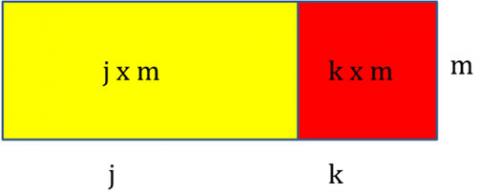
The 'boxed set' features arising here are:
equivalence
expressing situations
new from old
standard notation
Finally, to return to the 'missing number' situations I referred to earlier, it is useful to have 'missing numbers' that have to be found by reasoning rather than directly by number bonds. For example, finding missing lengths of sides of rectilinear compound shapes requires some reasoning about equality of opposite sides. Deriving unknown angles of a triangle or at a point requires
reasoning about the relations between angles you have already been told, and the missing one. This kind of reasoning can be extended to finding the coordinates of the vertices of squares and rectangles on coordinate grids, and being asked questions such as: Can these vertices form a square, and if so what is the missing vertex: ($a, b$); ($a$+2, $b$+2); ($a$+4, $b$)? In this final question
the 'boxed set' foci are:
expressing situations
standard notation
In summary ...
By following through these threads of algebraic thinking from early primary through to secondary formal algebra we can ensure that children's mathematical experiences follow a continuous progression.
Here is a PDF version of this article.
