Areas from Vectors
Use the applet to explore the area of a parallelogram and how it relates to vectors.
Problem
This resource is part of "Dotty Grids - Exploring Coordinates and Vectors"
Move the blue points below to change the vectors that define the parallelogram.
See how the area changes.
Explore how the area of the parallelogram changes as you change the vectors.
If you would like some ideas of interesting questions to explore, take a look below.
Is there a formula for the area of a parallelogram if I know the two vectors?
Why does the formula work?
What is the formula in the special case when the parallelogram is a square?
What is special about the areas of the rhombuses you can make?
Getting Started
Student Solutions
Tony computed the answers for some particular cases.
For $\mathbf{p}=\left(\begin{array}{c}3\\ 0\end{array}\right), \mathbf{q}=\left(\begin{array}{c}5 \\ 2\end{array}\right)$ the area is $6$ units squared ($=3\times 2-0\times 5$)
For $\mathbf{p}=\left(\begin{array}{c}3 \\ 2\end{array}\right), \mathbf{q}=\left(\begin{array}{c}0 \\ 4\end{array}\right)$ the area is $12$ units squared ($=3\times 4-2\times 0$)
For $\mathbf{p}=\left(\begin{array}{c}4 \\ 1\end{array}\right), \mathbf{q}=\left(\begin{array}{c}3 \\ 3\end{array}\right)$ the area is $9$ units squared ($=4\times 3-1\times 3$)
For $\mathbf{p}=\left(\begin{array}{c}2 \\ 4\end{array}\right), \mathbf{q}=\left(\begin{array}{c}-1 \\ 3\end{array}\right)$ the area is $10$ units squared ($=2\times 3-4\times (-1)$)
James, Jamie and George from Gillingham School sent us their formula for the area of the general parallelogram.
$$a d-b c\ \text{ (or } bc-ad\text{ if } bc>ad)$$
Here's one way to work that out.
Image
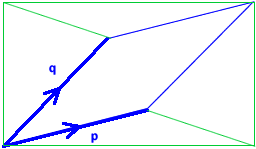
Remember that $\mathbf{p}=\left(\begin{array}{c}a \\ b\end{array}\right)$ and $\mathbf{q}=\left(\begin{array}{c}c\\d\end{array}\right)$.
The diagram shows the parallelogram inside a rectangle with base $a+c$ and height $b+d$. This rectangle has area $(a+c)(b+d)$. If we could find the areas of the triangles outside the parallelogram, then we could subtract them from the area of the rectangle to find the area of the parallelogram.
The bottom triangle has height $b$ and base $a+c$, so has area $\frac{1}{2}b(a+c)$.
The triangle on the left has (if you imagine it on its side so that its base is at the bottom) base $b+d$ and height $c$, so has area $\frac{1}{2}c(b+d)$.
The triangle at the top is congruent to the triangle at the bottom (it has been rotated by $180^{\circ}$), so has area $\frac{1}{2}b(a+c)$.
The triangle on the right is congruent to the triangle on the left, so has area $\frac{1}{2}c(b+d)$.
So the area of the parallelogram is $$(a+c)(b+d)-2\times\frac{1}{2}b(a+c) -2\times\frac{1}{2}c(b+d)=$$
$$a b+b c+a d+c d-a b-b c-b c-c d=a d-b c$$
$$a b+b c+a d+c d-a b-b c-b c-c d=a d-b c$$
just as James, Jamie and George said.
Yingtong Yan solved the problem differently, using stage 5 mathematics.
If we let $\mathbf{p}(x_1, y_1)$ and $\mathbf{q}(x_2, y_2)$ be our two vectors, then the cosinus of the angle between them is
$$\cos<\mathbf{p},\mathbf{q}>=\frac{\mathbf{p} \cdot \mathbf{q}}{|\mathbf{p}|\times |\mathbf{q}|}.$$
Therefore, $$\cos^2<\mathbf{p},\mathbf{q}>=\frac{(\mathbf{p} \cdot \mathbf{q})^2}{(|\mathbf{p}|\times |\mathbf{q}|)^2}$$
and, since $\sin^2<\mathbf{p},\mathbf{q}>+\cos^2<\mathbf{p},\mathbf{q}>=1$,
$$\sin^2<\mathbf{p},\mathbf{q}>=1 - \frac{(\mathbf{p} \cdot \mathbf{q})^2}{(|\mathbf{p}|\times |\mathbf{q}|)^2}= \frac{(|\mathbf{p}|\times |\mathbf{q}|)^2-(\mathbf{p} \cdot \mathbf{q})^2}{(|\mathbf{p}|\times |\mathbf{q}|)^2}.$$
Moreover, since the angle between $\mathbf{p}$ and $\mathbf{q}$ is smaller then $180^\circ$, then $\sin<\mathbf{p},\mathbf{q}>$ is greater then 0, and, hence, $\sin<\mathbf{p},\mathbf{q}> = \sqrt{\frac{(|\mathbf{p}|\times |\mathbf{q}|)^2-(\mathbf{p}\cdot\mathbf{q})^2}{(|\mathbf{p}|\times |\mathbf{q}|)^2} }$.
Using the fact that the parallelogram is made out of two congruent triangles of area $\frac{1}{2}\times\sin<\mathbf{p},\mathbf{q}>\times |\mathbf{p}|\times |\mathbf{q}|$, the area of the parallelogram is
$$\begin{aligned}
A_{\text{parallelogram}} &= 2\times \frac{1}{2}\times\sin<\mathbf{p},\mathbf{q}>\times |\mathbf{p}|\times |\mathbf{q}| \\
&= \sqrt{\frac{(|\mathbf{p}|\times |\mathbf{q}|)^2-(\mathbf{p}\cdot\mathbf{q})^2}{(|\mathbf{p}|\times |\mathbf{q}|)^2} }\times |\mathbf{p|}\times |\mathbf{q}| \\
&= \sqrt{ (|\mathbf{p}|\times |\mathbf{q}|)^2-(\mathbf{p}\cdot\mathbf{q})^2} \\
&= \sqrt{(x_1^2+y_1^2)\times (x_2^2+y_2^2) - (x_1x_2+y_1y_2)^2} \\
&=\sqrt{x_1^2y_2^2+x_2^2y_1^2-2x_1x_2y_1y_2} \\
&=|x_1y_2-x_2y_1|
\end{aligned}$$
Beth and Susie analyzed the special case when the parallelogram is a square.
If the parallelogram is a square then $|\mathbf{p}|=|\mathbf{q}|$ and the area is $|\mathbf{p}|^2$. Since $|\mathbf{p}|=\sqrt{a^2+b^2}$, the area is $\sqrt{a^2+b^2}^2=a^2+b^2$.
Well done to everyone who sent in a solution. Keep exploring!
Teachers' Resources
For ideas on how this problem and others from the Dotty Grids Collections can be used in the classroom, you may be interested to read this article.
