Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Subtended Angles
Age 11 to 14
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Arun from the National Public School in Bangalore sent us this detailed solution:
It is clearly seen that the angle at $C$ is twice the angle at $D$. Here we have the fundamental theorem with regard to angles in circles -" the angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the circle "
This can be proved as follows :
Given a circle $(C,r)$ in which arc $AB$ subtends angle ($ACB$) at the centre and angle ($ADB$) at any point $D$ on the circle.
To Prove:
(i) angle $(ACB)$ = $2\times$angle $(ADB)$, when arc $AB$ is a minor arc or a semicircle.
(ii) Reflex angle $(ACB) = 2\times$ angle $(ADB)$, when arc $AB$ is a major arc
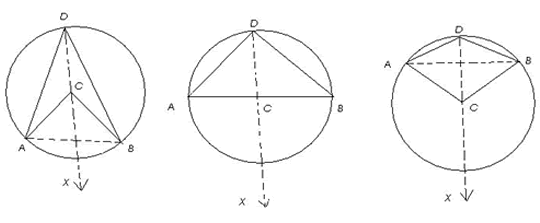
Construction: Join $AB$ and $DC$. Produce $DC$ to a point $X$ outside the circle.
Clearly, there are 3 cases.
Case I : arc $AB$ is a minor arc [Fig (i)]
Case II : arc $AB$ is a semicircle [Fig (ii)]
Case III : arc $AB$ is a major arc [Fig (iii)]
We know that when one side of a triangle is produced then the exterior angle so formed is equal to the sum of the interior opposite angles.
Therefore,
angle $(ACX)$ = angle $(CAD)$ + angle $(CDA)$ [consider triangle $CAD$]
angle $(BCX)$ = angle $(CBD)$ + angle $(CDB)$ [consider triangle $CBD$]
But,
angle $(CAD)$ = angle $(CDA)$ [since $CD = CA = r$ ] and ,
angle $(CBD)$ = angle $(CDB)$ [since $CD = CB = r$ ]
Therefore,
angle $(ACX) = 2\times$ angle $(CDA)$ and
angle $(BCX) = 2\times$angle $(CDB)$
In Fig (i) and Fig (ii) ,
angle $(ACX)$ + angle $(BCX)$ = $2 \times$ angle $(CDA)$ + $2\times$ angle $(CDB) \Rightarrow$
angle $(ACB)$ = $2$[angle $(CDA)$ + angle $(CDB)$] $\Rightarrow$
angle $(ACB)$ = $2 \times$angle $(ADB)$
in Fig (iii),
angle $(ACX)$ + angle $(BCX)$ = $2\times$ angle $(CDA)$ + $2\times$ angle $(CDB) \Rightarrow$
reflex angle $(ACB)$ = $2$[angle $(CDA)$ + angle $(CDB)$] $\Rightarrow$
reflex angle $(ACB)$ = $2\times $ angle $(ADB)$
Hence proved.
This theorem has 2 main implications:
(i) The angle in a semicircle is a right angle .
i.e. in fig (2), where arc $AB$ is a semicircle, or in other words $ACB$ is a diameter,
angle $(ADB) = \frac{1}{2} \times$ angle $(ACB) = \frac{1}{2}\times$($180$ degrees) = $90$ degrees = a right angle
This holds true for any position of point $C$ on the semicircle.
(ii) Angles in the same segment of a circle are equal.
This means that if an arc subtends $2$ angles, at $2$ different points on the circle, these angles will be equal.
We can prove this, by proving that each of the $2$ angles is equal to half the angle subtended at the centre.

