Routes 1 and 5
Find your way through the grid starting at 2 and following these
operations. What number do you end on?
Age
5 to 7
Challenge level
Problem
Image
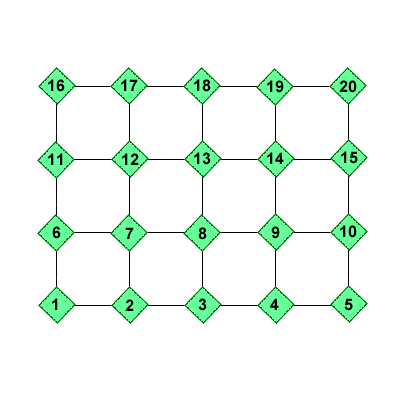
If you look at this grid you will see that when you move in different directions you add or subtract certain numbers. For example, moving one place to the right adds on one, moving up adds 5:
Image
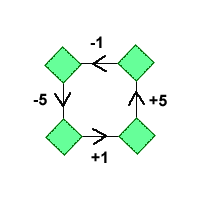
Find your way through the grid starting at 2 and following these operations:
Image
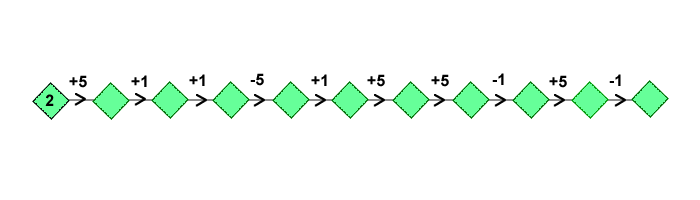
Find another way using these starting and end numbers, and record it in a similar way to the one above.
How can you use what you have done to find the shortest path between these two numbers?
Getting Started
Does the order of the route matter?
Does $+5 +5 +1$ get you to the same place as $+5 +1 +5$?
What about $+5 -5$ and $-5 +5$?
Student Solutions
Fiona from Tattingstone School tackled this very clearly:
Image
She found another way of starting and ending on these numbers:
Image
Fiona then explains:
Image
Omar from the Modern English School, Cairo drew out a few different routes which also start at $2$ and end at $18$:
Image
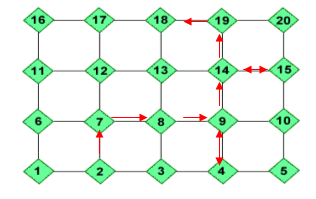
I like the way you've shown the 'optional extras' with double-headed arrows, Omar Abdel also from the Modern English School found another route:
$2+1+1+5-5+1+5+5-1+5-1$
Elliot, Richard and Christopher from Moorfield Junior School agreed with Fiona but also found another equally short route: $+1,+5,+5,+5$.
Molly and Callum from Bradon Forest School sent us a detailed response:
The last number in the sequence is $18$, and another Sequence is $2(+5)7(+5)12(+5)17(+1)18$.But the last one is the hardest. Still using the example
$2$-$18$ above you need to subtract the biggest number from the
smallest one ($18-2=16$)
The number you are left with is the number that all the steps
shold add up to, or 'special number' ($5+5+5+1=16$) or
($5+1+1-5+1+5+5-1+5-1=16$) To find out the number of steps and what
they are add keep adding together $5$'s until you reach the number
closest to the special number ($3\times5=15$ is closer to $16$ than
$4\times5=20$). Then continue adding or subtracting $1$'s until you
get the special number ($15+(1\times1)=16$). This might be a bit
clearer;
$3\times5 = 15$
$1\times1 = 01$ = $16$ --special number in four steps
You can try that on any sequence and it'll still work!!!
Luke from Witton Middle School noticed something important:
For the first part of the challenge, I worked out that the
number you ended on was $1$8.
So for the second part of the challenge, I did:
$2 +1 (3) +5 (8) -1 (7) +5 (12) -1 (11) +5 (16) +1 (17) -5
(12) +1 (13) +5 =18$
Then I used cancelling down (for example, $+1$ and $-1$ can be
cancelled out because whatever number is the input, the output will
be the same as the input. e.g. $32 +1 -1 =32$).
To end up with the shortest route - $2 +5 +5 +5 +1 =18$.
You could add in a different order but the answer would be the
same.
Well done, Luke, you're right that the order of the operations is not important - you would still get to $18$.
Teachers' Resources
Routes 1 and 5
Image
If you look at this grid you will see that when you move in different directions you add or subtract certain numbers. For example, moving one place to the right adds on one, moving up adds 5:
Image
Find your way through the grid starting at 2 and following these operations:
Image
Find another way using these starting and end numbers, and record it in a similar way to the one above.
How can you use what you have done to find the shortest path between these two numbers?
Why do this problem?
At its simplest, this is an exercise in mental addition and subtraction. But this problem also offers opportunities for discussions about inverse operations, a very important concept in mathematical thinking.
Possible approach
Display the grid and ask what the children notice about the numbers. Take all suggestions and make a note of them. Offer the first part of the question and ask the children on which number they end.
Allow some time for them to make up other routes that start on $2$ and end on $18$, and display them where everyone can see them..
Ask for a very long route
Ask for a very short route.
Invite children to explain what they notice is the same about all these routes and what is different.
Listen for reponses that connect the number of $+1$ and $-1$, and $+5$ and $-5$.
Allow some time for the children to make up their own routes for each other, choosing different starting and end points. Suggest that they make up a long route and give it to their partner, who does not look at the grid. The partner works out what the shortest route is (hopefully by matching $+1$ and $-1$, and $+5$ and $-5$) and together they check that both routes work on the grid.
Bring the children together and talk about the way that the numbers match - that they cancel each other out, that they are opposites, and introduce the word inverse if you think it appropriate.
If you have a large playground or school hall you could chalk out the grid on the floor and use the children themselves to play out the routes.
Key questions
What is the shortest route? How do you know?
What would a route look like that started and ended at the same place?
Could you write down a route that got you from the end back to the beginning, without looking at the grid?
Possible extension
You could offer children this sheet of two blank grids to make up their own set of numbers. Have they realised what the underlying structure of the numbers is?
The NNS program Monty uses the idea of hidden grids to reinforce visualisation. If you have internet access, or can download the software onto your system, some pupils will enjoy playing the game against the computer.