Walk and Ride
Problem
A group of $10$ students are on a field trip when their bus breaks down $40$ miles away from the school.
A teacher takes $5$ of them back to school in her car, travelling at an average speed of $40$ miles per hour.
The other $5$ students start walking towards school at a steady $4$ miles per hour.

The teacher drops the $5$ at school, then immediately turns around and comes back for the others, again travelling at a steady speed of $40$ miles per hour.
How far have the students walked by the time the car reaches them?
Getting Started
Work out all the fixed points - the times when you know the exact whereabouts of everybody, then think about each section separately.
You may want to alter the problem to use easier numbers, eg $30$ miles, $30$mph and $5$mph in order to find suitable methods to use on the main problem.
Student Solutions
This was a tough one, but several people took on the challenge! The answer 'about 7 miles' is a good answer, but three people managed to be even more exact.
The first step is to work out how far the students have walked by the time the car reaches the school.
Syed (Foxford School and Community College) explains:
"The car travels to school at a speed of 40 miles an hour.
The 5 students walked at a speed of 4 miles an hour.
So the car will take an hour to arrive at the school.
At the same time, the 5 students would have just done a 4 mile
walk.
The distance between the school/car and the 5 students should now
be
40 - 4 = 36 miles."
So the next step is find out when the returning car and the students will meet, and so find how much further the students will have walked. This is where people started thinking differently! See if you can follow their thinking.....
George (Rosebank Primary School, Leeds) says "If the car goes back 20 miles the students will be two miles nearer. Now there is fourteen miles between the car and the other five students. The teacher drives ten miles more and the students walk one mile. This time there is 3 miles between them. The students walk three elevenths of a mile and the car gets there exactly at the same time. I think the answer is that they meet at the seventh mile and three elevenths of a mile. " (This comes out as 7.27)
Thomas (Tattingstone School) says, "I worked this out by giving the distance the students walked a letter, in this case "L". I then worked out that however far the students walked, the car had gone ten times further. By the time the car had driven 5 students back to school, the other students had walked 4 miles. The rest of the distance that had to be travelled was 36 miles. Because the car goes ten times as far as the students, the number of L's to be travelled was 11. Then I worked out the number of 11's in 36, which was 3.27272727, rounded off and added to 4 which brought me to 7.27."
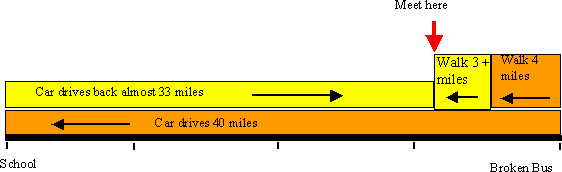
(George and Syed sent in similar diagrams to this. Drawings like this can be very helpful for working out problems)
Syed (Foxford School and Community College)
"The car then travelled at a speed of 40 miles an hour towards the students while at the same time the students are walking at a speed of 4 miles an hour. We have to find out how much distance the 5 students have to walk to be able to meet the car while the car is travelling.
All we have to do is to convert the speeds like this:
Car = A/B = 40 miles/an hour
5 students = C/D = 4 miles/an hour
We have to convert the two speeds so that A + C = 36, because this
is the distance between them, and so that B = D, because it must
take the car and the 5 students the same amount of time to be able
to travel to the part where they meet.
Car = 40 miles/an hour = 40 miles/60 minutes = about
33 miles/50 minutes
5 students = 4 miles/an hour = 4 miles/an hour = about
3 miles/50 minutes
33 + 3 = 36 miles
50 = 50" (This means the student walked about 4 + 3 = 7 miles)
Jessica (Tattingstone School) found another approach (with just a little help) to working out the 'bit more' the students might walk before the car arrived.
"......the teacher only has to drive back 36 miles but as she is travelling her 36 miles the students are still walking along at 4 miles per hour, making a combined speed of 44 miles per hur and they only have to travel 36 miles.
At 4 mph = 4/44 x 36 = 3.27 miles
At 40 mph = 40/44 x 36 = 32.73 miles
(Note: 3.27 + 32.73 = 36 miles)
So the students have walked (another) 3.27 by the time the car
reaches them".
Teachers' Resources
Why do this problem?
This problem provides some practice of working with distances, speeds and times, and it is accessible to students trying different cases numerically. It could also be an excellent moment to introduce distance-time graphs.
Possible approach
This printable worksheet may be useful: Walk and Ride.
Give out the details of the problem to students. You could have three or four variations of the problem - keeping the idea but altering the numbers. Allow plenty of time for them to work in pairs/groups trying out ideas and discussing how the methods can be improved.
As students come to solutions, ask them to work in pairs writing down their reasoning step by step. Solutions could be swapped with pairs from another group, on a different problem, to test how clearly the methods are explained! There are extension tasks available which may be appropriate here.
When the class have reached solutions and all are thoroughly familiar with the problem, stop them. Ask for feedback about the methods they used and how tricky the problem is. Suggest that we try representing the situation on a graph. Students can provide the details and scale for the time axis, explain that the vertical axis stands for distance from the site of the break down . Plot the progress of the teacher, slowly, asking questions/commenting about each point as it is plotted. Plot the walking students. Ask about all key features of the graph - the peak, the slopes, the intersection. Suggest that students might want to try out their earlier work with a graphical approach, or to see if it helps with the extension.
Key questions
When the teacher is there, where are the walking students?
At what time does the teacher drop off the first set of students?
ie tell me the fixed points - the times when you know the exact whereabouts of everybody.
Possible extension
Students may want to consolidate their thinking with a similar problem with slightly different speeds. Or to alter the current situation posing new problems for themselves.
A much more challenging extension task is:
The teacher gives the first bunch of students a lift but drops them off a bit before the school so they can walk the last bit. Meanwhile the teacher returns to pick up the other bunch of students who have been walking. At what time/distance must the teacher drop off the first students, so that all students arrive at the school at the same moment? Keep the speeds the same as for the original problem.
Possible support
Make the numbers easier -e.g. $30$mph and $5$mph and $30$ miles to school - and then make variations from there. Ensure that the description/discussion of the graph is really thorough. .
